Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét (O) có
ΔAMB nội tiếp đường tròn
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp đường tròn
AB là đường kính
Do đó: ΔANB vuông tại N
Xét (O) có
OH là một phần đường kính
MN là dây
OH\(\perp\)MN tại H
Do đó: H là trung điểm của MN
Xét ΔBMH vuông tại H và ΔBNH vuông tại H có
BH chung
MH=NH
Do đó: ΔBMH=ΔBNH
Suy ra: BM=BN
hay BN\(\in\)(B;BM)
Xét (B;BM) có
BM là bán kính
AM\(\perp\)BM tại M
Do đó: AM là tiếp tuyến của (B;BM)
Xét (B;BM) có
BN là bán kính
AN\(\perp\)BN tại N
Do đó:AN là tiếp tuyến của (B;BN)

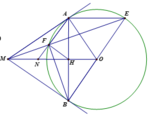
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn
Vẽ được các yếu tố để chứng minh phần (1).
Ta có M B O ^ = 90 0 , M A O ^ = 90 0 (theo t/c của tiếp tuyến và bán kính)
Suy ra: M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF. NA và MN = NH
Ta có A E / / M O ⇒ A E M ^ = E M N ^ mà A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^
Δ N M F v à Δ N A M có: M N A ^ chung; E M N ^ = M A F ^
nên Δ N M F đồng dạng với Δ N A M
⇒ N M N F = N A N M ⇒ N M 2 = N F . N A 1
Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N ^ h a y H B F ^ = F M H ^
=> MFHB là tứ giác nội tiếp
⇒ F H M ^ = F B M ^ = F A B ^ h a y F H N ^ = N A H ^
Xét Δ N H F & Δ N A H c ó A N H ^ c h u n g ; N H F ^ = N A H ^
=> Δ N M F đồng dạng Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A 2
Từ (1) và (2) ta có NH = HM
3) Chứng minh: H B 2 H F 2 − EF M F = 1 .
Xét Δ M AF và Δ M E A có: A M E ^ chung, M A F ^ = M E A ^
suy ra Δ M AF đồng dạng với Δ M E A
⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2 (3)
Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^ = B F H ^
Δ A E F và Δ H B F có: E F A ^ = B F H ^ ; F E A ^ = F B A ^
suy ra Δ A E F ~ Δ H B F
⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2 (4)
Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1

1/
Xét (O) có
\(\widehat{AMB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AM\perp BM\) => AM là tiếp tuyến với (B) bán kính BM
Ta có
\(AB\perp MN\Rightarrow MH=NH\) (trong đường tròn đường kính vuông góc với dây cung thì chia đôi dây cung tại điểm giao cắt)
=> AB vừa là đường cao vừa là đường trung tuyến của tg BMN
=> tg BMN cân tại B (Trong tg đường cao xp từ 1 đỉnh đồng thời là đường trung tuyến thì tg đó là tg cân tại đỉnh đó)
=> BM=BN (cạnh bên tg cân) => \(N\in\left(B\right)\) => BN là đường kính của (B)
Xét (O) có
\(\widehat{ANB}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AN\perp BN\)
=> AN là tiếp tuyến của (B)
2/
Ta có
\(MN=MH+NH\)
\(\Rightarrow MN^2=MH^2+NH^2+2.MH.NH\) (1)
Xét tg vuông AMB có
\(MH^2=AH.HB\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông bằng tích giữa các hình chiếu của 2 cạnh góc vuông trên cạnh huyền) (2)
\(\Rightarrow MH=\sqrt{AH.HB}\) (3)
Xét tg vuông ANB có
\(NH^2=AH.HB\) (lý do như trên) (4)
\(\Rightarrow NH=\sqrt{AH.HB}\) (5)
Từ (3) và (5) \(\Rightarrow MH.NH=\sqrt{AH.HB}.\sqrt{AH.HB}=AH.HB\) (6)
Thay (2) (4) (6) vào (1)
\(\Rightarrow MN^2=AH.HB+AH.HB+2.AH.HB=4.AH.HB\)

1: ΔOMN cân tại O
mà OA vuông góc MN
nên OA là trung trực của MN
=>AM=AN
góc AMB=góc ANB=1/2*sđ cung AB=90 độ
Xét ΔAMB vuông tại M và ΔANB vuông tại N có
AB chung
AM=AN
=>ΔAMB=ΔANB
=>BM=BN
=>AM,AN là tiếp tuyến của (B;BM)
2: MH^2=AH*HB
=>4*MH^2=4*AH*HB
=>MN^2=4*AH*HB
3: góc MBA=90-60=30 độ
=>góc MBN=60 độ
=>ΔMBN đều