Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ACB=1/2*sđ cung AB=90 độ
góc EIB+góc ECB=180 độ
=>EIBC nội tiếp
b: Sửa đề: AE*AC-AI*AB=0
Xét ΔAIE vuông tại I và ΔACB vuông tại C co
góc IAE chung
=>ΔAIE đồng dạng với ΔACB
=>AI/AC=AE/AB
=>AI*AB=AE*AC
=>AI*AB-AE*AC=0

1) Vì AB là đường kính \(\Rightarrow\angle ACB=90\)
\(\Rightarrow\angle ECB+\angle EIB=90+90=180\Rightarrow IECB\) nội tiếp
2)Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Ta có: \(\angle AME=90-\angle MAB=\angle ABM=\angle ACM\) (ABCM nội tiếp)
Xét \(\Delta AME\) và \(\Delta ACM:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACM\\\angle CAMchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACM\left(g-g\right)\)
3) Vì IECB nội tiếp \(\Rightarrow\angle IBK=\angle ECK\)
Xét \(\Delta EKC\) và \(\Delta IKB:\) Ta có: \(\left\{{}\begin{matrix}\angle IKB=\angle EKC\\\angle IBK=\angle ECK\end{matrix}\right.\)
\(\Rightarrow\Delta EKC\sim\Delta IKB\left(g-g\right)\Rightarrow\dfrac{EK}{IK}=\dfrac{EC}{IB}\Rightarrow EK.IB=EC.IK\)
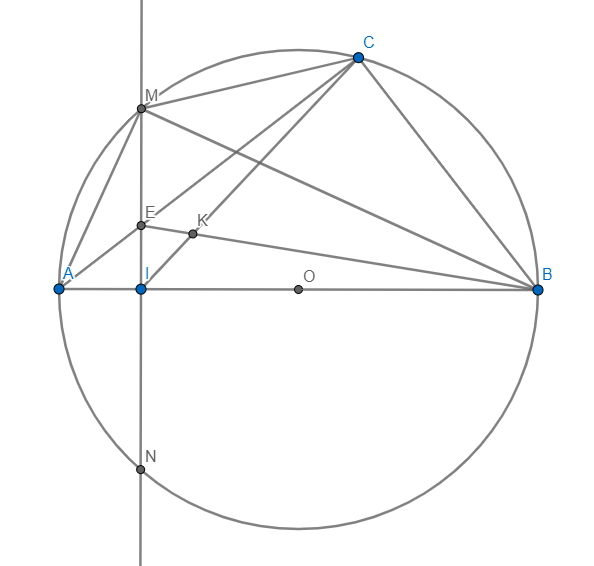

a: góc ACB=1/2*sđ cung AB=90 độ
góc EIB+góc ECB=180 độ
=>ECBI nội tiếp đường tròn đường kính EB
Tâm là trung điểm của EB
b: Xét ΔANE và ΔACM có
góc ANE=góc ACM(=1/2sđ cung AM)
góc NAE=góc CAM
=>ΔANE đồng dạng với ΔACM

c, Mình không vẽ được hình nên bạn thông cảm Gọi tâm đường tròn ngoại tiếp tam giác CME là K
Từ câu b : AM^2=AE.AC
Mà AC là cát tuyến của đường tròn ngoại tiếp tam giác CME
=> AM là tiếp tuyến của đường tròn ngoại tiếp tam giác CME
=> \(AM\perp MK\)
Mà \(AM\perp MB\)
=> M,K,B thẳng hàng
=> \(K\in MB\)cố định
Khi đó để NKmin thì K là hình chiếu của N lên MB
Đến đây bạn tự tính NK nhé
Sau đó từ MK để xác định điểm C

c)
5. Theo trên: \(\widehat{AMN}=\widehat{ACM}\)
=> AM là tiếp tuyến của đường tròn ngoại tiếp \(\Delta\) ECM;
Nối MB ta có\(\widehat{AMB}\)= 900 , do đó tâm O1 của đường tròn ngoại tiếp\(\Delta\)ECM phải nằm trên BM
. Ta thấy NO1 nhỏ nhất khi NO1 là khoảng cách từ N đến BM => NO1 \(\perp\)BM.
Gọi O1 là chân đường vuông góc kẻ từ N đến BM ta được:
O1 là tâm đường tròn ngoại tiếp D ECM có bán kính là O1M.
Do đó để khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất thì C phải là giao điểm của đường tròn tâm O1 bán kính O1M với đường tròn (O) trong đó O1 là hình chiếu vuông góc của N trên BM.