Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giao điểm của (d) và (C) thỏa mãn:
\(\left(2+t\right)^2+\left(-1+3t\right)^2-2\left(2+t\right)-1=0\)
\(\Leftrightarrow10t^2-4t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=\dfrac{2}{5}\end{matrix}\right.\)
Vậy (d) và (C) cắt nhau tại 2 điểm có tọa độ là: \(\left[{}\begin{matrix}\left(2;-1\right)\\\left(\dfrac{12}{5};\dfrac{1}{5}\right)\end{matrix}\right.\)

Vì phương trình tham số của (d) là \(\left\{{}\begin{matrix}x=1+t\\y=2-3t\end{matrix}\right.\)
nên (d) đi qua B(1;2) và có vecto chỉ phương là (1;-3)
=>Vecto pháp tuyến là (3;1)
Phương trình tổng quát của (d) là:
3(x-1)+1(y-2)=0
=>3x-3+y-2=0
=>3x+y-5=0
Vì (d') vuông góc với (d) nên (d') có dạng là:
x-3y+c=0
Thay x=2 và y=-1 vào (d'), ta được:
2+3+c=0
hay c=-5

1: (d): x=-2-2t và y=1+2t nên (d) có VTCP là (-2;2)=(-1;1) và đi qua B(-2;1)
=>(d') có VTPT là (-1;1)
Phương trình (d') là;
-1(x-3)+1(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
2: (d) có VTCP là (-1;1)
=>VTPT là (1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+y+1=0
Tọa độ H là;
x+y+1=0 và -x+y+2=0
=>x=1/2 và y=-3/2

a: vtpt là (4;3)
Phương trình tổng quát là:
4(x-1)+3(y-2)=0
=>4x-4+3y-6=0
=>4x+3y-10=0
b: Phương trình Δ là:
2(x+2)+3(y-4)=0
=>2x+4+3y-12=0
=>2x+3y-8=0
c: Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có:
\(\left\{{}\begin{matrix}-2a+b=1\\3a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{5}\\b=\dfrac{7}{5}\end{matrix}\right.\)
d: Vì (d1)//(d) nên (d1): 3x-5y+c=0
Thay x=4 và y=-2 vào (d1), ta được:
c+3*4-5*(-2)=0
=>c=-22
f: (d): 2x-7y-1=0
=>Δ: 7x+2y+c=0
Thay x=3 và y=5 vào Δ, ta được:
c+21+10=0
=>c=-31

Hiện tại là characters và symbols của mình ko bấm được bạn ạ, máy tính mình hư mang đi sửa rồi, gợi ý thôi nhé :))
Câu a đơn giản thôi, bạn viết véctơ AB ra, nghĩa là lúc này, đường thẳng đi qua 2 điểm AB có véctơ chủ phương là AB, bạn viết véctơ pháp tuyến ra là được, rồi chọn 1 trong 2 điểm A,B làm x0,y0 là ok rồi :))
Còn câu b, trước hết là bạn phải viết ptđt của delta đã, trong sgk có instructions đó :)
Rồi sau đó, như mình đã nói với bạn hồi chiều, 2 đt song song thì có chung véctơ pháp tuyến, giờ bài toán chỉ cong là: viết ptđt đi qua điểm A và có véctơ pháp tuyến là...
Đơn giản thôi hà :D

\(\left\{{}\begin{matrix}x=2+t\\y=1-3t\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6+3t\\y=1-3t\end{matrix}\right.\) \(\Rightarrow3x+y=7\Rightarrow3x+y-7=0\)
Vậy (d) có pt tổng quát là: \(3x+y-7=0\)
A và B nằm cùng phía đối với d khi và chỉ khi:
\(\left(3.1+2-7\right)\left(3.\left(-2\right)+m-7\right)>0\)
\(\Leftrightarrow-2\left(m-13\right)>0\)
\(\Rightarrow m< 13\)
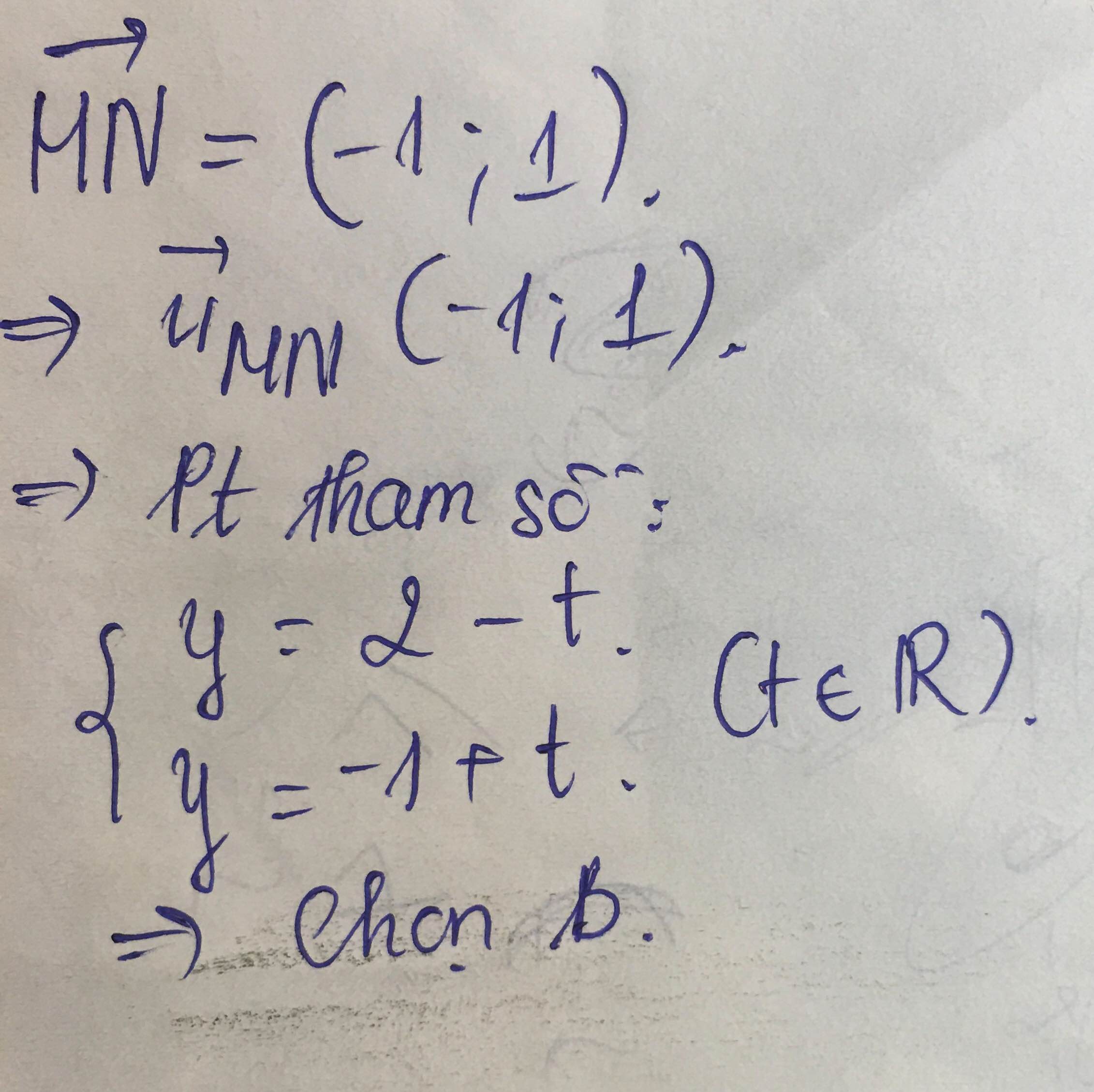
\(A\in d\Rightarrow A\left(-2+t;-1+3t\right)\)
\(AB=\sqrt{10}\Leftrightarrow\sqrt{\left(-2+t-2\right)^2+\left(-1+3t-1\right)^2}=\sqrt{10}\)
\(\Leftrightarrow\left(t-4\right)^2+\left(3t-2\right)^2=10\\ \Leftrightarrow t^2-8t+16+9t^2-12t+4=10\\ \Leftrightarrow10t^2-20t+20=10\\ \Leftrightarrow t^2-2t+1=0\Leftrightarrow\left(t-1\right)^2=0\Leftrightarrow t=1\)
\(\Rightarrow A\left(-1;2\right)\).