Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

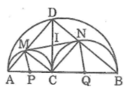
Tam giác ABD nội tiếp trong đường tròn có AB là đường kính nên ![]() = 90o hay
= 90o hay ![]() =
90
°
=
90
°
Tam giác ACM nội tiếp trong đường tròn có AC là đường kính nên ![]() =
90
°
=
90
°
Suy ra: CM ⊥ AD ⇒ ![]() =
90
°
=
90
°
Tam giác BCN nội tiếp trong đường tròn có AC là đường kính nên ![]() =
90
°
=
90
°
Suy ra: CN ⊥ BD ⇒  =
90
°
=
90
°
Tứ giác CMDN có ba góc vuông nên nó là hình chữ nhật

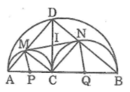
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên ![]() (3)
(3)
Tam giác CNQ cân tại Q nên ![]() (4)
(4)
Vì AB ⊥ CD nên ![]() =
90
°
(5)
=
90
°
(5)
Từ (3), (4) và (5) suy ra: ![]() =
90
°
hay MN ⊥ QN
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên 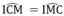 (6)
(6)
Tam giác CMP cân tại P nên 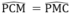 (7)
(7)
Vì AB ⊥ CD nên 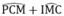 =
90
°
(8)
=
90
°
(8)
Từ (6), (7) và (8) suy ra: 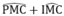 =
90
°
hay MN ⊥ PM
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC

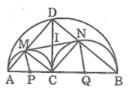
Tam giác ACD vuông tại C có CM ⊥ AD
Theo hệ thức lượng trong tam giác vuông, ta có:
C D 2 = DM.DA (1)
Tam giác BCD vuông tại C có CN ⊥ BD
Theo hệ thức lượng trong tam giác vuông, ta có:
C D 2 = DN.DB (2)
Từ (1) và (2) suy ra: DM.DA = DN.DB

a: góc AMC=1/2*180=90 độ
=>góc DMC=90 độ
góc CNB=1/2*180=90 độ
=>góc DNC=90 độ
Kẻ tiếp tuyến Cx của hai đường tròn đường kính AC,CB, Cx cắt MN tại I
Xét (E) có
IC,IM là tiếp tuyến
=>IC=IM
Xét (F) có
IN,IC là tiếp tuyến
=>IN=IC=IM
Xét ΔMCN có
CI là trung tuyến
CI=MN/2
=>ΔMCN vuông tại C
góc DMC=góc DNC=góc MCN=90 độ
=>DMCN là hcn
b: ΔDCA vuông tại C có CM vừa là đường cao
nên DM*DA=DC^2
ΔDCB vuông tại C có CN là đường cao
nên DN*DB=DC^2=DM*DA

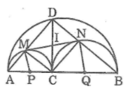
Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: CD ≤ OD nên MN ≤ OD
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.

Bài 1:
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi



k biết thì hỏi. Vấn đề gì à