Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

UC = max \(\rightarrow\) cộng hưởng \(\rightarrow\) UR = U = 220 V
\(U_{Lmax}\rightarrow\overrightarrow{U}\text{⊥}\overrightarrow{U_{RC}}\rightarrow U^2_L=U^2+U^2_{RC}\)\(=U^2+U^2_R+U^2_C\rightarrow275^2=220^2+132^2+U^2_C\)\(\rightarrow U_C=99V\)
\(Chọn.D\)

Khi L = L 1 điện áp hiệu dụng trên tụ cực đại → cộng hưởng, khi đó U = U R = 200 V .
Khi L = L 2 điện áp trên cuộn dây cực đại, ta có U R C = U L m a x 2 − U 2 = 189 V .
→ Điện áp hiệu dụng trên tụ U C = U R C 2 − U R 2 = 135 V .
Đáp án B

Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
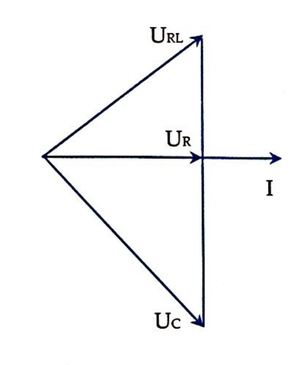
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.


Đáp án B
+ Với ω = ω 1 thì điện áp hiệu dụng ở hai đầu tụ điện đạt giá trị cực đại
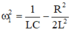
và
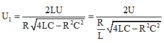
+ Với
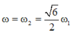
thì điện áp hiệu dụng ở hai đầu điện trở đạt giá trị cực đại
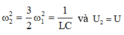
Mặc khác
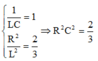
+ Khi
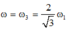
điện áp hiệu dụng trên hai đầu tụ điện là
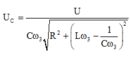
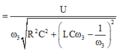
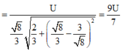
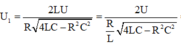
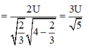
Từ đó ta tìm được
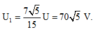

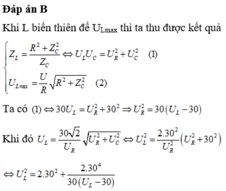
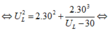
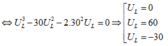


Đáp án D
Khi L = L1, UC max => mạch xảy ra cộng hưởng UR = U = 220V.
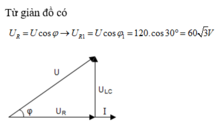
Khi L = L2, UL max => u vuông pha với uRC. Ta có giản đồ vecto:
Áp dụng hệ thức lượng trong tam giác: