Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện trở tương đương của mạch là:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{6\cdot3}{6+3}=\dfrac{18}{9}=2\Omega\)

Đáp án D
Điện trở mạch mắc song song
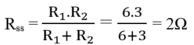
Cường độ dòng điện I = U/R = 6/2 = 3A

Điện trở tương đương của mỗi đoạn mạch:
+) ( R 1 nt R 2 ) // R 3 :
R 12 = R 1 + R 2 = 6 + 12 = 18Ω
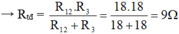
+) ( R 3 nt R 2 ) // R 1 :
R 23 = R 2 + R 3 = 12 + 18 = 30Ω
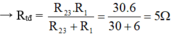
+) ( R 1 nt R 3 ) // R 2 :
R 13 = R 1 + R 3 = 6 + 18 = 24Ω
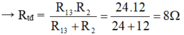

a) Vì điện trở R 1 / / R 2 nên R t đ = ( R 1 . R 2 ) / ( R 1 + R 2 ) = ( 9 . 6 ) / ( 9 + 6 ) = 3 , 6 Ω .
b) Tính cường độ dòng điện
Cường độ dòng điện qua mạch chính là: I = U/R = 7,2/3,6 = 2A
Cường độ dòng điện qua R 1 là: I 1 = U / R 1 = 7,2/9 = 0,8A.
Cường độ dòng điện qua R 2 là: I 2 = U / R 2 = 7,2/6 = 1,2A.

a) Điện trở tương đương là:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}}=\dfrac{1}{\dfrac{1}{12}+\dfrac{1}{6}+\dfrac{1}{4}}=2\left(\Omega\right)\)
b) Hiệu điện thế U:
\(U=I.R=3.2=6\left(V\right)\)

MCD: R1//R2
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{60\cdot120}{60+120}=40\left(\Omega\right)\)
tóm tắc
\(R_1=R_2=6\left(\text{ Ω}\right)\)
\(R_{tđ}=?\)
Giải
Điện trở tương đương của đoạn mạch là:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{6.6}{6+6}=3\left(\text{Ω}\right)\)
Đáp số : \(R_{tđ}=3\text{Ω}\)
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{6\cdot6}{6+6}=3\left(\text{Ω}\right)\)