Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔODE cân tại O có OI là trung tuyến
nên OI vuông góc DE
góc OIA=góc OBA=90 độ
=>OIBA nội tiếp
b: Xét (O) có
AC,AB là tiếp tuyến
=>AC=AB
mà OB=OC
nên OA là trung trực của BC
=>BC vuông góc OA tại H
=>AH*AO=AB^2
Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE=AH*AO

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\)
b: Ta có: \(\widehat{ABI}+\widehat{OBI}=\widehat{OBA}=90^0\)
\(\widehat{HBI}+\widehat{OIB}=90^0\)(ΔHBI vuông tại H)
mà \(\widehat{OBI}=\widehat{OIB}\)
nên \(\widehat{ABI}=\widehat{HBI}=\widehat{CBI}\)
=>BI là phân giác của góc ABC
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AO là phân giác của góc BAC
Xét ΔBAC có
AH,BI là các đường phân giác
AH cắt BI tại I
Do đó: I là tâm đường tròn nội tiếp ΔBAC
a, Để chứng minh \(OH \times OA = \pi^2\), chúng ta có thể sử dụng định lí thứ ba của đường tròn và định lí Euclid về tiếp tuyến và tiếp tuyến ngoại tiếp.
Gọi \(R\) là bán kính của đường tròn, \(O\) là tâm của đường tròn, \(A\) là điểm nằm ngoài đường tròn, \(B\) và \(C\) là các điểm tiếp tuyến từ \(A\) đến đường tròn. \(H\) là giao điểm giữa \(OA\) và \(BC\).
Theo định lí thứ ba của đường tròn, ta có \(OH\) là đoạn trung bình của \(OA\) trong tam giác \(OAB\). Điều này có nghĩa là \(OH\) là trung bình hòa của các phần bằng nhau \(OA\) và \(OB\).
\(OA = OB = R\) (bán kính của đường tròn).
\(OH = \frac{OA + OB}{2} = \frac{2R}{2} = R\).
Vậy, \(OH = R\).
Để chứng minh \(OH \times OA = \pi^2\), ta có \(OH \times OA = R \times R = R^2\).
Nhưng theo định nghĩa, \(R\) là bán kính của đường tròn, nên \(R^2\) chính là \(\pi^2\) (bán kính mũ hai). Vì vậy, \(OH \times OA = \pi^2\).
b, Để chứng minh \(I\) là tâm của đường tròn nội tiếp tam giác \(ABC\), chúng ta có thể sử dụng các định lí về tiếp tuyến và tiếp tuyến ngoại tiếp.
Gọi \(I\) là giao điểm của \(OA\) với đường tròn. Khi đó, theo định lí về tiếp tuyến ngoại tiếp, \(OA\) vuông góc với \(AB\) tại \(B\) và \(OA\) vuông góc với \(AC\) tại \(C\).
Vì OA là đường trung trực của BC (do H là giao điểm giữa OA và BC, nên OH cũng là đường trung trực của BC.)
Nếu I là tâm của đường tròn nội tiếp tam giác ABC, thì OI cũng là đường trung trực của BC
Do đó, OHvà OI là cùng một đường trung trực của BC, nên OH = OI.
Vậy, I là tâm của đường tròn nội tiếp tam giác ABC.

a) Vì AB,AC là tiếp tuyến \(\Rightarrow\Delta ABC\) cân tại A có AO là phân giác \(\angle BAC\)
\(\Rightarrow OA\bot BC\)
Xét \(\Delta ABD\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle ABD=\angle AEB\\\angle EABchung\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
b) tam giác ABO vuông tại B có đường cao BH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=AH.AO\Rightarrow AH.AO=AD.AE\Rightarrow\dfrac{AH}{AE}=\dfrac{AD}{AO}\)
Xét \(\Delta AHD\) và \(\Delta AEO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AH}{AE}=\dfrac{AD}{AO}\\\angle EAOchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHD\sim\Delta AEO\left(c-g-c\right)\Rightarrow\angle AHD=\angle AEO\Rightarrow DEOH\) nội tiếp
c) Ta có: \(\angle BHE=90-\angle OHE=90-\angle ODE\) (DEOH nội tiếp)
\(=90-\dfrac{180-\angle DOE}{2}=\dfrac{1}{2}\angle DOE=\dfrac{1}{2}\angle DHE\) (DEOH nội tiếp)
\(\Rightarrow HB\) là phân giác \(\angle DHE\Rightarrow\dfrac{ID}{IE}=\dfrac{DH}{HE}\)
Vì HB là phân giác \(\angle DHE\) và \(HA\bot HB\Rightarrow HA\) là phân giác ngoài \(\angle DHE\)
\(\Rightarrow\dfrac{AD}{AE}=\dfrac{DH}{HE}=\dfrac{ID}{IE}\Rightarrow AD.IE=ID.AE\)
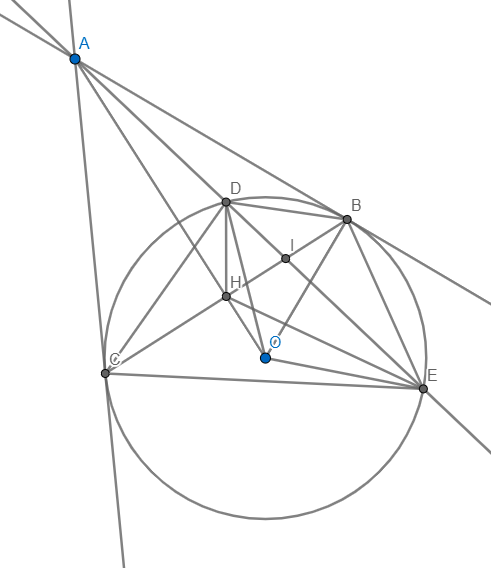
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC tại H
Xét ΔADB và ΔABE có
\(\widehat{BAD}\) chung
\(\widehat{ABD}=\widehat{AEB}\left(=\dfrac{1}{2}sđ\stackrel\frown{BD}\right)\)
Do đó: ΔADB\(\sim\)ΔABE(g-g)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{AB}{AE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AD\cdot AE\)

chứng minh tứ giác OBDK nội tiếp:
dựa vào góc DBK=DOK (vì hai góc cùng chắn cung DK)
vậy, ta cần chứng minh DBK=DOK
đặt giao của OM với AB là H
dễ dàng chứng minh: DBK=BOA=1/2 BOC (1)
có M thuộc (O) và tiếp tuyến CD của M nên chứng minh được tam giác OBD=OMD (ch,cgv)
=> góc BOD=DOM và MOE=COE (chứng minh tương tự)
=> DOM+EOM=DOE=1/2BOM+1/2MOC=1/2BOC (2)
từ (1),(2) => DOK=KBD (đpcm)

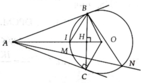
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

a) Xét tứ giác IAOB có
\(\widehat{IAO}\) và \(\widehat{IBO}\) là hai góc đối
\(\widehat{IAO}+\widehat{IBO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: IAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn \(\stackrel\frown{AC}\)
\(\widehat{IAC}\) là góc tạo bởi tiếp tuyến AI và dây cung AC
Do đó: \(\widehat{ADC}=\widehat{IAC}\)(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
hay \(\widehat{IDA}=\widehat{IAC}\)
Xét ΔIDA và ΔIAC có
\(\widehat{IDA}=\widehat{IAC}\)(cmt)
\(\widehat{AIC}\) chung
Do đó: ΔIDA∼ΔIAC(g-g)
Suy ra: \(\dfrac{ID}{IA}=\dfrac{IA}{IC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(IA^2=IC\cdot ID\)(đpcm)

a) C/m tg ABCO nội tiếp:
+) Ta có: góc ACO = 90•( vì AC là tiếp tuyến đg tròn (O))
góc ABO = 90•( vì AB là tiếp tuyến đg tròn (O))
+) Xét tg ABOC có: góc ACO+ góc ABO=90•+90•=180•
Mà 2 góc ở vị trí đối nhau
=> tg ABOC nội tiếp đg tròn(dhnb)
b) C/m: CD// AO:
+) Vì AB và AC là 2 tiếp tuyến cắt nhau tại A(gt) => AO là đg pg của góc COB( t/c 2 tiếp tuyến cắt nhau)
=> AO là pg của tam giác COB
Mà tam giác COB cân tại O( OB=OC=R)
=> OA là đg cao của tam giác COB( t/c tam giác cân)
=> OA vuông góc vs CB( t/c) (1)
+) Xét (O) ta có:
BD là đg kính( gt)
góc BCD là góc nội tiếp chắn cung BD
=> góc BCD= 90• ( t/c góc nội tiếp chắn nửa đg tròn)
=> CD vuông góc vs CB(t/c) (2)
Từ(1) và (2) suy ra: CD// OA( từ vuông góc đến song song).
mk chưa ra câu c nên xin lỗi bn nhiều nhé....