Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A, ta có:
AB2 + AC2 = BC2 <=> 122 + 162 = 400 => BC=20 (BC>0)
Vì AD là đường phân giác góc A => \(\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}\) (tính chất đường phân giác trong tam giác)
<=>\(\frac{BD}{3}=\frac{CD}{4}=\frac{BD+CD}{3+4}=\frac{BC}{7}=\frac{20}{7}\)( tính chất dãy tỉ số bằng nhau )
Khi đó: BD = \(\frac{20}{7}.3\)=\(\frac{60}{7}\) ; CD = \(\frac{20}{7}.4\)=\(\frac{80}{7}\)
b) Ta có: tam giác ABH ~ tam giác CBA (\(\widehat{BAC}=\widehat{BHA}=90^0\); \(\widehat{B}\)chung)
=> \(\frac{AB}{BC}=\frac{BH}{AB}\)<=> AB2= BH.BC <=> BH=\(\frac{AB^2}{BC}\)= \(\frac{12^2}{20}\)=\(\frac{36}{5}\)=7,2 (cm)
Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H, ta có:
BH2 + AH2 = AB2 <=> AH2 + 7,22 = 122 <=> AH = \(\frac{48}{5}=9,6\)(cm)
HD = BD - BH = \(\frac{60}{7}-7,2\)=\(\frac{48}{35}\)(cm)
Áp dụng định lí Py-ta-go vào tam giác AHD vuông tại H, ta có:
AH2 + HD2 = AD2 <=> 9,62 + \(\left(\frac{48}{35}\right)^2\)= AD2 <=> AD = \(\frac{48\sqrt{2}}{7}\)(cm)

Do bạn SSBĐ Love HT làm được câu a) rồi nên mình làm nốt câu b) còn lại nhé :
a) Ta tính được : \(BC=20cm,BD=DC=10cm\)
b) Do \(\Delta ABC\) vuông ở A, có \(AH\perp BC\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\cdot AB\cdot AC=\frac{1}{2}\cdot AH\cdot BC\)
\(\Leftrightarrow12\cdot16=AH\cdot20\)
\(\Leftrightarrow AH=\frac{48}{5}\left(cm\right)\)
Áp dụng định lý Pytago cho các tam giác vuông ta có :
+) \(\Delta ABH\) vuông tại H \(\Rightarrow AB^2=AH^2+BH^2\)
\(\Leftrightarrow12^2=\left(\frac{48}{5}\right)^2+BH^2\)
\(\Leftrightarrow BH=\frac{36}{5}\left(cm\right)\)
\(\Rightarrow HD=BD-BH=10-\frac{36}{5}=\frac{14}{5}\left(cm\right)\)
+) \(\Delta AHD\) vuông tại H \(\Rightarrow AD^2=AH^2+HD^2\)
\(\Rightarrow AD^2=\left(\frac{48}{5}\right)^2+\left(\frac{14}{5}\right)^2\)
\(\Rightarrow AD=10cm\)
Vậy : \(AH=\frac{48}{5}\left(cm\right),HD=\frac{14}{5}\left(cm\right),AD=10\left(cm\right)\)
a)ΔABC vuông tại A
Áp dụng định lí Pitago:
⇒ BC=\(\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20cm\)
AD là tia phân giác ta có:
\(\frac{AB}{AC}\)=\(\frac{BD}{DC}\)Hay \(\frac{AB}{AC}\)=\(\frac{BD}{BC-BD}\)=\(\frac{12}{16}\)=\(\frac{3}{4}\)
\(\Rightarrow\frac{BD}{20-BD}\)=\(\frac{3}{4}\)\(\rightarrow\)4BD=60-3BD⇒ BD=8\(\times\)6cm
⇒ CD=BC-BD=20-8,6=11,4cm
b)Xét ΔAHB và ΔABC
\(\widehat{CAB}\)là góc chung
\(\widehat{AHB}=\widehat{ABC}\)
⇒ΔAHB đồng dạng ΔABC
\(\frac{AH}{AC}\)=\(\frac{AB}{AC}\)
⇒AH=\(\frac{AC\times AB}{BC}\)=\(\frac{16-12}{20}\)=\(9,6cm\)
Áp dụng hệ thức lượng : BH=\(\frac{36}{5}\);\(CH=\frac{64}{5}\)
⇒ HD=BD-BH=8\(\times\)6−\(\frac{36}{5}\)=1,4cm
ΔDHA vuông tại H
⇒AD=\(\sqrt{AH^2+HD^2}=\sqrt{9\times6^2+1\times4^2}=9,7cm\)
Đáp án:a)BC=20cm; BD=8.6cm; CD=11,4cm
b)AH=9.6cm; HD=1.4cm; AD=9.7cm

a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).

a) Áp dụng định lý Pi-ta-go vào \(\Delta\)vuông ABC có :
\(AB^2+AC^2=BC^2\Leftrightarrow BC=20\left(cm\right)\)
Do AD là phân giác \(\widehat{A}\)theo tính chất đường phân giác , ta có :
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}\)
\(\Rightarrow\frac{BD}{BD+CD}=\frac{3}{3+4}\Rightarrow\frac{BD}{BC}=\frac{3}{7}\)
\(\Rightarrow BD=\frac{3}{7}BC=\frac{60}{7}\)
\(\Rightarrow DC=BC-BD=\frac{80}{7}\)
b) AH là đường cao \(\Delta\)vuông ABC nên :
\(S_{\Delta ABC}=\frac{AH.BC}{2}=\frac{AB.AC}{2}\)
\(\Rightarrow AH=\frac{AB.C}{BC}=\frac{48}{5}\left(cm\right)\)
Ta có :
\(BH^2=AB^2-AH^2\Rightarrow BH=\frac{36}{5}\left(cm\right)\)
\(\Rightarrow DH=BD=BH=\frac{48}{35}\left(cm\right)\)
\(AD^2=DH^2+AH^2\Rightarrow AD=\frac{48\sqrt{2}}{7}\left(cm\right)\)

a)Xét tam giác ABC có A=90
\(BC=\sqrt{AB^2+AC^2}=\sqrt{16^2+12^2}=20\left(cm\right)\)
Mà AD là tia phân giác BAC nên\(\frac{AB}{BD}=\frac{AC}{CD}\)
Áp dụng tính chất dãy tỉ số bằng nhau ,ta có:
\(\frac{AB}{BD}=\frac{AC}{CD}=\frac{AB+AC}{BD+CD}=\frac{7}{5}\)
\(\Rightarrow BD=\frac{60}{7}\left(cm\right),\\CD=\frac{80}{7}\left(cm\right)\)
b) Dễ c.m được \(\Delta ABH\)đồng dạng với \(\Delta CBA\)
\(\Leftrightarrow\frac{AB}{CB}=\frac{BH}{BA}=\frac{AH}{CA}\Leftrightarrow\frac{12}{20}=\frac{BH}{12}=\frac{AH}{16}\)
\(\Rightarrow BH=\frac{36}{5}\left(cm\right),\\ AH=\frac{48}{5}\left(cm\right)\\ \Rightarrow CH=\frac{64}{5}\left(cm\right)\)
Mà CD=80/7 nên HD=48/35(cm)
Xét AHD vuông tại H
nên\(AD=\sqrt{\frac{48}{35}^2+\frac{48}{5}^2}=\frac{48\sqrt{2}}{7}\left(cm\right)\)
Nếu có sai mong bạn thông cảm nha

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
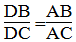
Suy ra:
Suy ra:
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)

Xét \(\Delta ABC\) vuông tại A có \(AB^2+AC^2=BC^2\) (định lý Pytago)
\(\Rightarrow BC^2=12^2+16^2=20^2\Rightarrow BC=20\).
Theo tính chất đường phân giác trong tam giác ABC ta có:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{CD+BD}{AC+AB}=\dfrac{BC}{AC+AB}=\dfrac{20}{12+16}=\dfrac{5}{7}\Rightarrow BD=\dfrac{60}{7};CD=\dfrac{80}{7}\).
Ta có \(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{5}\).
Từ đó \(BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-\left(\dfrac{48}{5}\right)^2}=\dfrac{36}{5}\).
Suy ra \(HD=\left|BD-BH\right|=\left|\dfrac{48}{5}-\dfrac{36}{5}\right|=\dfrac{12}{5}\).
\(AD=\sqrt{AH^2+HD^2}=\dfrac{12\sqrt{17}}{5}\).

a: ΔACB vuông tại A co AH vuông góc BC
nên AB^2=BH*BC
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=16/8=2
=>AD=6cm

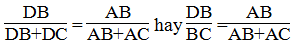
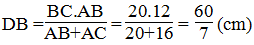
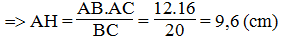
Lời giải:
a) Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=20$ (cm)
Theo tính chất đường phân giác:
$\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BC}=\frac{3}{7}\Rightarrow BD=BC.\frac{3}{7}=20.\frac{3}{7}=\frac{60}{7}$ (cm)
$CD=BC-BD=\frac{80}{7}$ (cm)
b)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD=BD-BH=\frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD=\sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
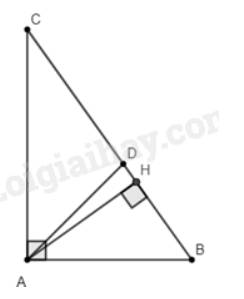
Hình vẽ: