Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi S là giao của BM với d, N là giao của BP với HK
Xét ΔPAM và ΔOBM có
AP/MA=OB/MB
góc PAM=góc OBM
=>ΔPAM đồng dạng với ΔOBM
=>PA/PM=OB/OM=1
=>PA=PM
góc AMS=90 độ
=>góc PAM+góc PSM=90 độ=góc PMA+góc PMS
PM=PA
=>góc PSM=góc PMS
=>PS=PM
=>PA=PS
KH//AS
=>NK/PA=BN/BP=NH/PS
=>NK=NH
=>BP đi qua trung điểm của HK

click vào đường giải dưới đây
hình 9 | Diễn đàn HOCMAI - Cộng đồng học tập lớn nhất Việt Nam

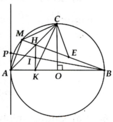
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)