Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha!
Sửa lại đề là \(CF=EB.\)
a) Ta có:
\(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{ABE}=180^0\\\widehat{ACB}+\widehat{ACF}=180^0\end{matrix}\right.\) (các góc kề bù).
Mà \(\widehat{ABC}=\widehat{ACB}\left(gt\right)\)
=> \(\widehat{ABE}=\widehat{ACF}.\)
b) Xét 2 \(\Delta\) \(ABE\) và \(ACF\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{ABE}=\widehat{ACF}\left(cmt\right)\)
\(BE=CF\left(gt\right)\)
=> \(\Delta ABE=\Delta ACF\left(c-g-c\right).\)
c) Theo câu b) ta có \(\Delta ABE=\Delta ACF.\)
=> \(\widehat{AEB}=\widehat{AFC}\) (2 góc tương ứng).
Hay \(\widehat{HEB}=\widehat{KFC}.\)
Xét 2 \(\Delta\) vuông \(EBH\) và \(FCK\) có:
\(\widehat{BHE}=\widehat{CKF}=90^0\left(gt\right)\)
\(EB=FC\left(gt\right)\)
\(\widehat{HEB}=\widehat{KFC}\left(cmt\right)\)
=> \(\Delta EBH=\Delta FCK\) (cạnh huyền - góc nhọn) (đpcm).
Chúc bạn học tốt!

a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy của ΔBAC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE(gt)
\(\widehat{HDB}=\widehat{KEC}\)(ΔADB=ΔAEC)
Do đó: ΔHBD=ΔKCE(cạnh huyền-góc nhọn)
c) Ta có: ΔHBD=ΔKCE(cmt)
nên \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\)
Xét ΔHDB vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHDB=ΔKEC
Suy ra: BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
Do đó: ΔAHB=ΔAKC

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔADB=ΔAEC
=>AD=AE
=>ΔADE cân tại A
b,c: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>BH=CK
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc MAB=góc NAC(góc MAB=góc MAC+góc BAC;góc NAC=góc NAB+góc BAC;gócMAC=góc NAB)
=>ΔAMB=ΔANC
=>BM=CN
d: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
=>HK//BC

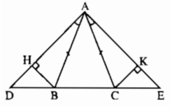
Xét tam giác BHA và ∆CKA có
∠AHB = ∠AKC = 90º
AB = AC ( vì tam giác ABC cân tại A).
∠HAB = ∠KAC ( giả thiết)
Suy ra ΔBHA = ΔCKA (cạnh huyền – góc nhọn), suy ra BH = CK.


Sửa đề: Lấy E thuộc tai đối của tia BC,Lấy F thuộc tia đối của tia CB sao cho CF = EB
Giải
a/Có: \(\widehat{ABC}+\widehat{ABE}=180^0\)
\(\widehat{ACB}+\widehat{ACF}=180^0\)
Lại có: \(\widehat{ABC}=\widehat{ACB}\left(GT\right)\)
=> \(\widehat{ABE}=\widehat{ACF}\)
b/ Xét ΔABE và ΔACF ta có:
AB = AC (GT)
\(\widehat{ABE}=\widehat{ACF}\) (câu a)
EB = CF (GT)
=> ΔABE = ΔACF (c - g - c)
c/ Có: ΔABE = ΔACF (câu a)
=> \(\widehat{AEB}=\widehat{AFC}\) (2 góc tương ứng)
Hay: \(\widehat{HEB}=\widehat{KFC}\)
Xét ΔHBE và ΔKCF ta có:
EB = CF (GT)
\(\widehat{HEB}=\widehat{KFC}\) (cmt)
=> ΔHBE = ΔKCF (c.h - g.n)