Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(5x2+5y2+8xy-2x+2y+2=0\)
(=) \((4x^2 + 8xy + 4y^2) + (x^2 - 2x +1) + (y^2 + 2y +1) = 0 \)
(=) \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
Ta có \(\begin{cases} 4(x+y)^2 ≥ 0 \\ (x-1)^2 ≥ 0 \\ (y+1)^2 ≥ 0 \end{cases} \)
=> \(4(x+y)^2 + (x-1)^2 + (y+1)^2 ≥ 0 \)
Vậy để \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
(=) \(\begin{cases} 4(x+y)^2 = 0 \\ (x-1)^2 = 0 \\ (y+1)^2 = 0 \end{cases} \)
(=) \(\begin{cases} x = -y \\ x = 1 \\ y = -1 \end{cases} \)
(=) \(\begin{cases} x = 1 \\ y = -1 \end{cases} \)
Vậy \(M=(x+y)^{2015}+(x-2)^{2016}+(y+1)^{2017} M=(1-1)^{2015} + (1-2)^{2016} + (-1+1)^{2017} M=0^{2015} + (-1)^{2016} +0^{2017} M= 1 \)Vậy M = 1

kho....................wa..................troi.......................thi.....................ret.................lanh................wa..................tich............................ung.........................ho..............minh......................cho....................do....................lanh
Ta có: 5x2+5y2+8xy-2x+2y+2=0
=> 4x2+8xy+4y2+x2-2x+1+y2+2y+1=0
=> (2x+2y)2+(x-1)2+(y+1)2=0
=> {2x+2y=0 => x=-y
{x-1 = 0 => x=1
{y+1 =0 => y=-1
=> x=1, y=-1
Thay vào biểu thức M, ta có:
M=(1+-1)2015+(1-2)2016+(-1+1)2017=0+1+0=1 (đpcm)

Ta có: 5x2 + 5y2 + 8xy - 2x + 2y = 0
\(\Leftrightarrow\)(4x2 + 4y2 + 8xy) + (x2 - 2x + 1) + (y2 + 2y + 1) = 0
\(\Leftrightarrow\)(2x + 2y)2 + (x - 1)2 + (y + 1) = 0
\(\Leftrightarrow\)\(\hept{\begin{cases}2x+2y=0\\x-1=0\\y+1=0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=1\\y=-1\end{cases}}\)
Thay vào pt ta đc:
M = (x + y)2015 + (x - 2)2016 + (y + 1)2017
= (1 - 1)2015 + (1 - 2)2016 + (-1 + 1)2017 = 1

Sửa đề: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{{}\begin{matrix}2x+2y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x-y\right)^{2023}-\left(x-2\right)^{2024}+\left(y+1\right)^{2023}\)
\(=\left(1+1\right)^{2023}-\left(1-2\right)^{2024}+\left(-1+1\right)^{2023}\)
\(=2^{2023}-1\)

Ta có 5x2+5y2+8xy-2x+2y+2=0
=> (4x2+8xy+4y2)+(x2-2x+1)+(y2+2y+1)=0
=> (2x+2y)2+(x-1)2+(y+1)2=0
=> (2x+2y)2=(x-1)2=(y+1)2=0
=> x=1 và y=-1
=> M=(x+y)2015+(x-2)2016+(y+1)2017
=(1-1)2015+(1-2)2016+(-1+1)2017
= 0+(-1)2016+0
=1
tính M=(x+y)2015+(x-2)2016+(y+1)2017
Ta có
5x^2 + 5y^2 + 8xy - 2x + 2y + 2= 0
<=> 4x^2 + 8xy + 4y^2 + x^2 - 2x + 1 + y^2 + 2y + 1 = 0
<=> (4x^2 + 8xy + 4y^2) + (x^2 - 2x + 1) + (y^2 + 2y + 1) =0
<=> (2x + 2y)^2 + (x - 1)^2 + (y + 1)^2 =0
<=> 2x + 2y= 0 hoặc x - 1= 0 và y + 1= 0
<=> x=1 và y= - 1 thay x=1, y= - 1 vào biểu thức M ta có
M= (1 - 1)^2015 + (1 - 2)^2016 + ( - 1 + 1)^2017
= 0 + - 1^2016 + 0 = 1

\(5x^2+5y^2+8xy-2x+2y+2=0\)
\(\Leftrightarrow\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\)
\(\Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
Ta thấy \(VT\ge VP\forall x;y\) để đấu "=" xảy ra \(\Leftrightarrow x=1;y=-1\) thay vào M :
\(M=\left(-1+1\right)^{2015}+\left(1-2\right)^{2016}+\left(-1+1\right)^{2017}=1\)

b: 5x^2+5y^2+8xy-2x+2y+2=0
=>4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0
=>(x-1)^2+(y+1)^2+(2x+2y)^2=0
=>x=1 và y=-1
M=(1-1)^2015+(1-2)^2016+(-1+1)^2017=1
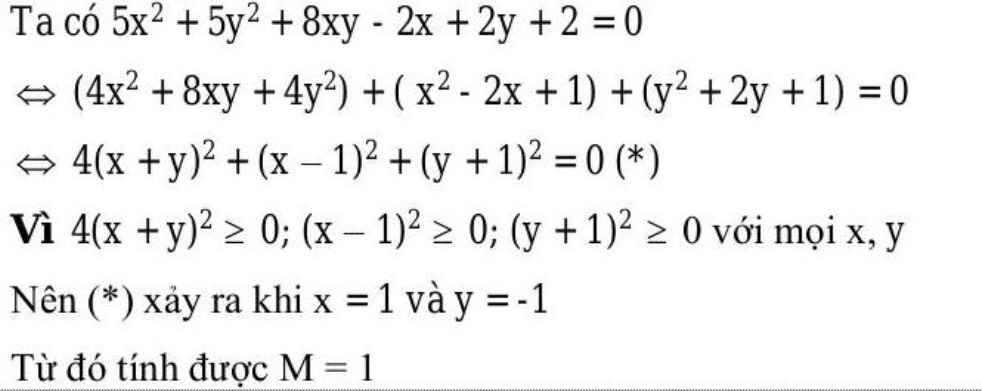
5x2 + 5y2 + 8xy - 2x + 2y + 2 = 0
\(\Leftrightarrow\)(4x2 + 8xy + 4y2) + (x2 - 2x + 1) + (y2 + 2y + 1) = 0
\(\Leftrightarrow\)(2x + 2y)2 + (x - 1)2 + (y + 1)2 = 0
\(\Leftrightarrow\)\(\hept{\begin{cases}2x+2y=0\\x-1=0\\y+1=0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=-y\\x=1\\y=-1\end{cases}}\)
M = (x + y)2015 + (x - 2)2016 + (y + 1)2017
= 0 + (1 - 2)2016 + 0 = 1