Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
a: \(A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b: Để A=3 thì 3x-9=x+1
=>2x=10
hay x=5
Bài 2:
a: \(A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}\)
b: Để A nguyên thì \(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;1;5;-1\right\}\)
a) \(A=\frac{2x}{x+3}+\frac{2}{x-3}+\frac{x^2-x+6}{9-x^2}\left(x\ne\pm3\right)\)
\(\Leftrightarrow A=\frac{2x}{x+3}+\frac{2}{x-3}-\frac{x^2-x+6}{x^2-9}\)
\(\Leftrightarrow A=\frac{2x}{x+3}+\frac{2}{x-3}-\frac{x^2-x+6}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow A=\frac{2x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}+\frac{2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{x^2-x+6}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow A=\frac{2x^2-6x+2x+6-x^2+x-6}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow A=\frac{x^2-3x}{\left(x-3\right)\left(x+3\right)}=\frac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\frac{x}{x+3}\)
Vậy \(A=\frac{x}{x+3}\left(x\ne\pm3\right)\)
b) Ta có \(A=\frac{x}{x+3}\left(x\ne\pm3\right)\)
Để A nhạn giá trị nguyên thì \(\frac{x}{x+3}\)nhận gái trị nguyên
Ta có \(\frac{x}{x+3}=\frac{x+3-3}{x+3}=1-\frac{3}{x+3}\)
=> \(\frac{3}{x+3}\)nguyên thì \(1-\frac{3}{x+3}\)nguyên
=> 3 chia hết cho x+2.
x nguyên => x+3 nguyên => x+3\(\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Ta có bảng
| x+3 | -3 | -1 | 1 | 3 |
| x | -6 | -4 | -2 | 0 |
Đối chiếu điều kiện x\(\ne\pm3;x\inℤ\)
=> x={-6;-4;-2;0}
Vậy x={-6;-4;-2;0} thì A nhận giá trị nguyên
a: Thay x=-4 vào B, ta được:
\(B=\dfrac{-4+3}{-4}=\dfrac{-1}{-4}=\dfrac{1}{4}\)
b: \(P=A\cdot B=\dfrac{x^2-3x+2x-9+3x+9}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}\)
\(=\dfrac{x^2+2x}{\left(x-3\right)}\cdot\dfrac{1}{x}=\dfrac{x+2}{x-3}\)
c: Để P nguyên thì \(x-3\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{4;2;8;-2\right\}\)
\(\frac{x+2}{x+3}-\frac{5}{x^2+x-6}+\frac{1}{2-x}=\frac{x+2}{x+2}+\frac{-5}{x^2+x-6}+\frac{-1}{x-2}\)
=\(\frac{\left(x+2\right)\left(x-2\right)}{x^2+x-6}+\frac{-5}{x^2+x-6}+\frac{-1\left(x+3\right)}{x^2+x-6}=\frac{\left(x+2\right)\left(x-2\right)-5-1\left(x+3\right)}{x^2+x-6}\)
=\(\frac{x^2-4-5-x-3}{x^2+x-6}=\frac{x^2-x-12}{x^2+x+6}\)
\(\frac{x^2-x-12}{x^2+x-6}=\frac{x^2-x-12}{\left(x-2\right)\left(x+3\right)}\)
Để giá trị của PT A được xác định thì \(\left(x-2\right)\ne0\)và \(\left(x+3\right)\ne0\)
=> \(x\ne2\) và \(x\ne-3\) thì PT được xác định
\(a,đk\left(B\right):x\ne\pm3\\ B=\dfrac{3}{x-3}-\dfrac{6x}{9-x^2}+\dfrac{x}{x+3}\\ =\dfrac{3}{x-3}+\dfrac{6x}{x^2-9}+\dfrac{x}{x+3}\\ =\dfrac{3\left(x+3\right)+6x+x\left(x-3\right)}{x^2-9}\\ =\dfrac{3x+9+6x+x^2-3x}{x^2-9}\\ =\dfrac{x^2+6x+9}{x^2-9}\\ =\dfrac{\left(x+3\right)^2}{x^2-9}\\ =\dfrac{x+3}{x-3}\)
\(b,P=A.B\\ =\dfrac{x+1}{x+3}\times\dfrac{x+3}{x-3}\\ =\dfrac{x+1}{x-3}\)
\(c,\) Để P nguyên
\(\dfrac{x+1}{x-3}=1+\dfrac{4}{x-3}\)
=> \(x-3\inƯ\left(4\right)\)
\(Ư\left(4\right)=\left\{-1;1;2;-2;4;-4\right\}\)
\(=>x=\left\{2;4;5;1;7;-1\right\}\)
Bài 1:
a.\(\left(x+y\right)^2-\left(x-y\right)^2=\left(x+y-x+y\right)\left(x+y+x-y\right)=2\left(x+y\right)\)
b.\(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2+\left(x-y\right)^2=\left(x+y+x-y\right)^2=4x^2\)
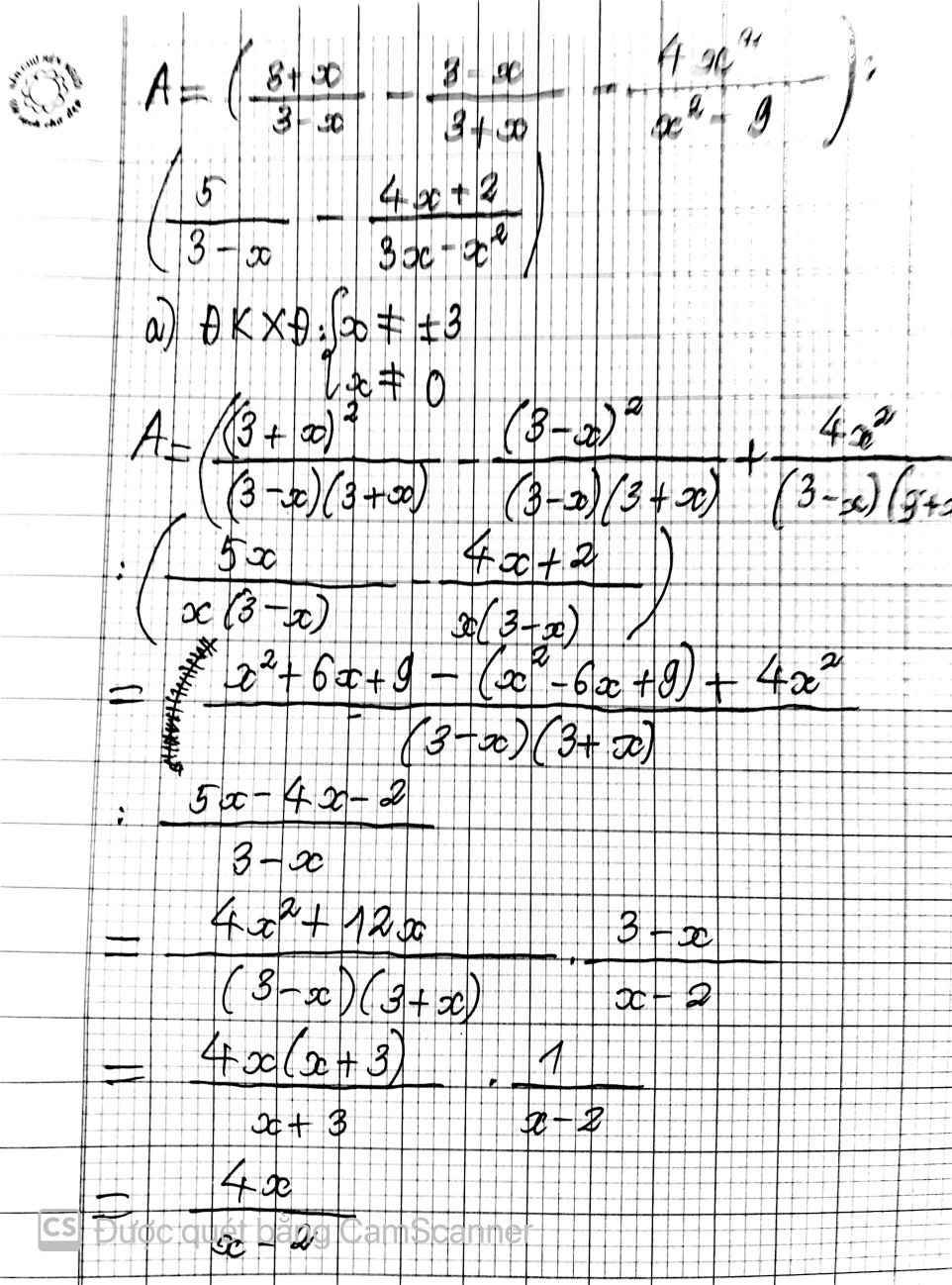
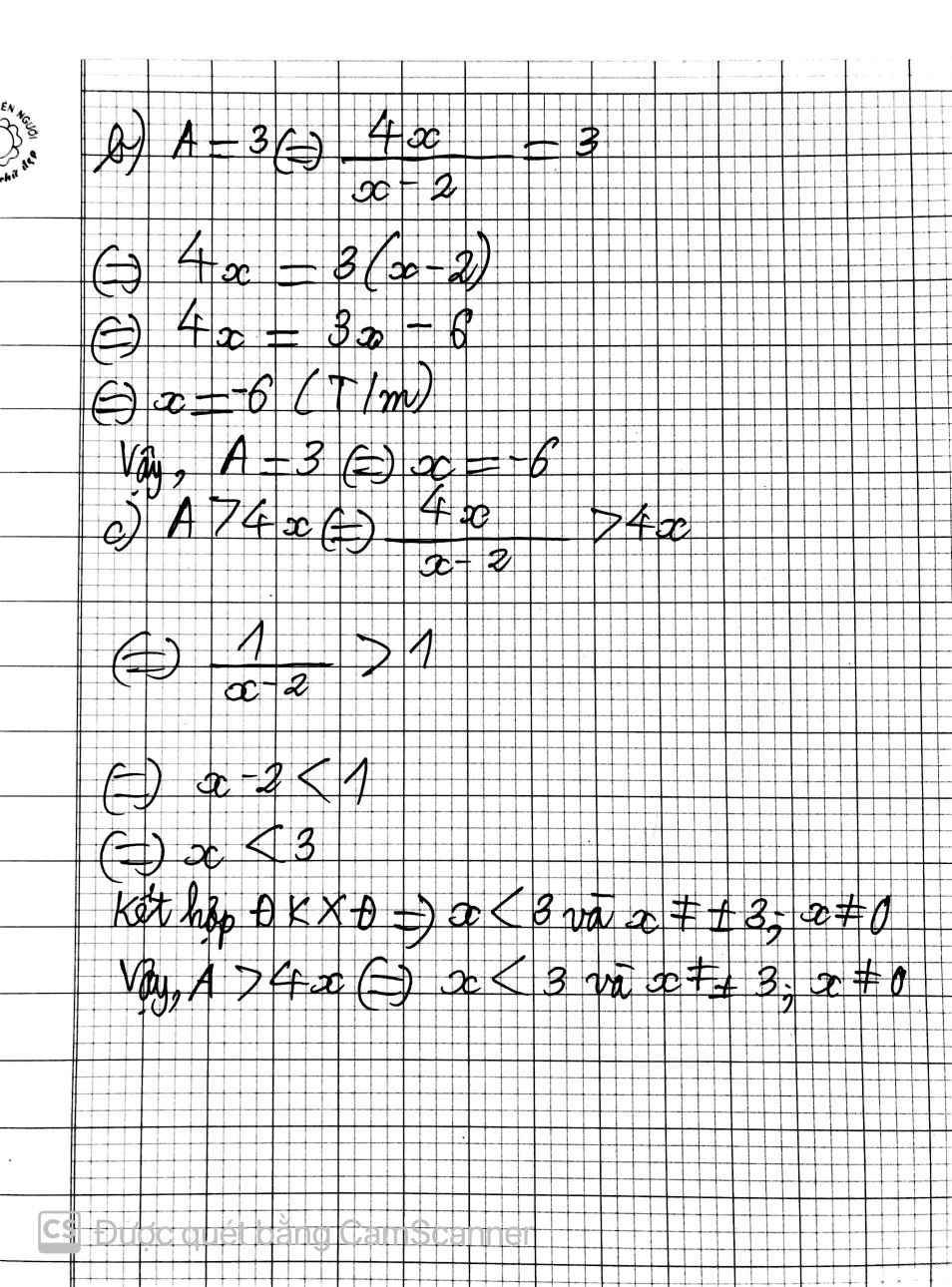
Điều kiện: x ≠ 0; x ≠ 1 và x ≠ 3