Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt vế trái BĐT cần chứng minh là P
Ta có:
\(P=\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a^2}{\sqrt{2\left(b^2+c^2\right)}}+\dfrac{b^2}{\sqrt{2\left(a^2+c^2\right)}}+\dfrac{c^2}{\sqrt{2\left(a^2+b^2\right)}}\)
Đặt \(\left(\sqrt{b^2+c^2};\sqrt{c^2+a^2};\sqrt{a^2+b^2}\right)=\left(x;y;z\right)\Rightarrow x+y+z=\sqrt{2011}\)
Đồng thời: \(\left\{{}\begin{matrix}y^2+z^2-x^2=2a^2\\z^2+x^2-y^2=2b^2\\x^2+y^2-z^2=2c^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{y^2+z^2-x^2}{2}\\b^2=\dfrac{z^2+x^2-y^2}{2}\\c^2=\dfrac{x^2+y^2-z^2}{2}\end{matrix}\right.\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{y^2+z^2-x^2}{x}+\dfrac{z^2+x^2-y^2}{y}+\dfrac{x^2+y^2-z^2}{z}\right)\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{y^2+z^2}{x}+\dfrac{z^2+x^2}{y}+\dfrac{x^2+y^2}{z}-\left(x+y+z\right)\right)\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{\left(y+z\right)^2}{2x}+\dfrac{\left(z+x\right)^2}{2y}+\dfrac{\left(x+y\right)^2}{2z}-\left(x+y+z\right)\right)\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{\left(y+z+z+x+x+y\right)^2}{2x+2y+2z}-\left(x+y+z\right)\right)=\dfrac{1}{2\sqrt{2}}\left(x+y+z\right)=\dfrac{1}{2}\sqrt{\dfrac{2011}{2}}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\sqrt{\dfrac{2011}{2}}\)

The nesbit: cái điều trên luôn đúng
Có nhiều cách cm nesbit:
Cauchy-Schwarz
AM-GM
Cách gì cũng dùng được cả. GG để tìm hiểu thêm nhé bạn
:)) giúp có tâm vờ lun giải ik siêng chút ik beengs vậy soan ày làm sao :))

Ta có: \(\dfrac{a^2}{b^2}+1\ge2\sqrt{\dfrac{a^2}{b^2}}=\dfrac{2a}{b}\)
Tương tự: \(\dfrac{b^2}{c^2}+1\ge\dfrac{2b}{c}\) ; \(\dfrac{c^2}{a^2}+1\ge\dfrac{2c}{a}\)
\(\Rightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}+3\ge\dfrac{2a}{b}+\dfrac{2b}{c}+\dfrac{2c}{a}\) (1)
Mà \(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge3\sqrt[3]{\dfrac{abc}{abc}}=3\)
\(\Rightarrow\dfrac{2a}{b}+\dfrac{2b}{c}+\dfrac{2c}{a}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+3\) (2)
(1);(2) \(\Rightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}+3\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+3\)
\(\Rightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\)
Dấu "=" xảy ra khi \(a=b=c\)

-Áp dụng BĐT Caushy Schwarz ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{a+b+c}=\dfrac{9}{1}=9\)
-Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Cjo 3 số dương a,b,c . CMR
\(\dfrac{a^2}{b+c}+\dfrac{b^2}{a+c}+\dfrac{c^2}{a+b}\ge\dfrac{a+b+c}{2}\)

Do a,b,c dương
Để làm bài này bạn cần chứng minh BĐT sau\(\dfrac{x^2}{m}+\dfrac{y^2}{n}\ge\dfrac{\left(x+y\right)^2}{m+n}\)(m;n>0)
<=>(m+n)(nx2+my2)-mn(x+y)2\(\ge\)0
Mình làm tắt,rút gọn luôn
<=>n2x2-2mnxy+m2y2\(\ge\)0
<=>(nx-my)2\(\ge\)0
=>BĐT trên được chứng minh và dấu bằng xảy ra khi nx=my
Mở rộng cho 3 số \(\dfrac{x^2}{m}+\dfrac{y^2}{n}+\dfrac{z^2}{p}\ge\dfrac{\left(x+y+z\right)^2}{m+n+p}\)
Áp dụng BĐT trên ta được:
\(\dfrac{a^2}{b+c}+\dfrac{b^2}{a+c}+\dfrac{c^2}{a+b}\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}\)
Dấu = xảy ra khi a=b=c
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)

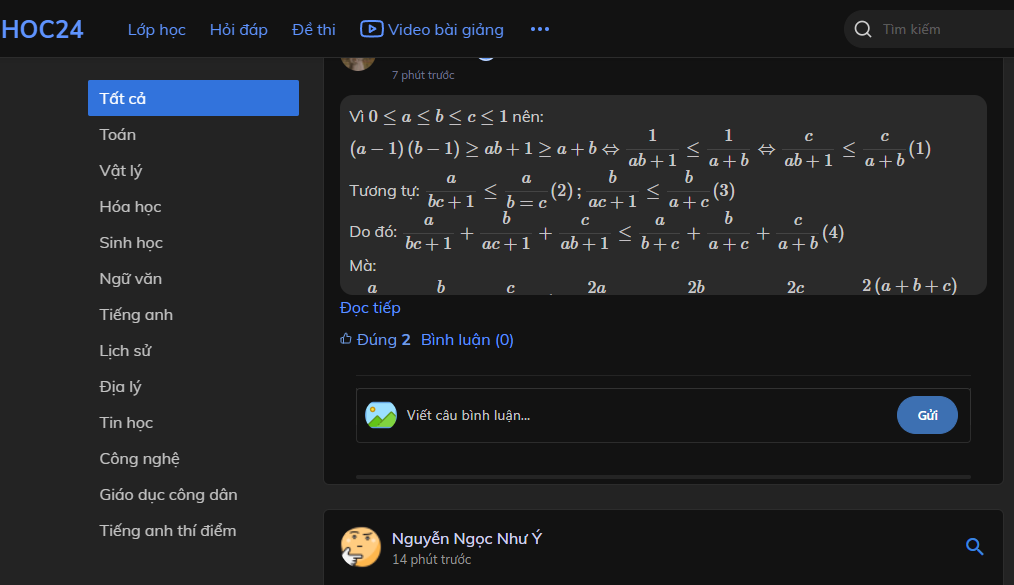
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)

\(VT=\dfrac{\left(a+c\right)^2}{\left(a+c\right)\left(a+b\right)}+\dfrac{\left(b+d\right)^2}{\left(b+c\right)\left(b+d\right)}+\dfrac{\left(c+a\right)^2}{\left(c+a\right)\left(c+d\right)}+\dfrac{\left(d+b\right)^2}{\left(d+a\right)\left(d+b\right)}\)
\(VT\ge\dfrac{\left(2a+2b+2c+2d\right)^2}{\left(a+b\right)\left(a+c\right)+\left(b+c\right)\left(b+d\right)+\left(a+c\right)\left(c+d\right)+\left(a+d\right)\left(b+d\right)}=\dfrac{4\left(a+b+c+d\right)^2}{\left(a+b+c+d\right)^2}=4\)
Dấu "=" xảy ra khi \(a=b=c=d\)
A = \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\)
A = \(\dfrac{a^2}{a\left(b+c\right)}+\dfrac{b^2}{b\left(a+c\right)}+\dfrac{c^2}{c\left(a+b\right)}\)
Áp dụng BĐT Cô - Si dạng Engel vào bài toán , ta có :
\(\dfrac{a^2}{a\left(b+c\right)}+\dfrac{b^2}{b\left(a+c\right)}+\dfrac{c^2}{c\left(a+b\right)}\) ≥ \(\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ac\right)}\) ( * )
Ta lại có BĐT : x2 + y2 + z2 ≥ xy + yz + zx
⇒ a2 + b2 + c2 ≥ ab + bc + ac
⇔ ( a + b + c)2 ≥ 3( ab + bc + ac)
⇔ \(\dfrac{\left(a+b+c\right)^2}{ab+bc+ac}\) ≥ 3 ( **)
Từ ( *;**) ⇒ \(\dfrac{a^2}{a\left(b+c\right)}+\dfrac{b^2}{b\left(a+c\right)}+\dfrac{c^2}{c\left(a+b\right)}\) ≥ \(\dfrac{3}{2}\)
⇒ \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\) ≥ \(\dfrac{3}{2}\)
Đời về cơ bản là buồn... cười!!!Phùng Khánh LinhHong Ra Onchú tuổi gìNguyễn Ngô Minh TríNhã Doanh, và nhiều bạn khác...