Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

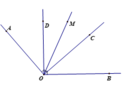
a) Ta có O C ⊥ O A nên A O C ^ = 90 ° ; O D ⊥ O B nên B O D ^ = 90 ° .
Tia OD nằm trong góc AOB nên A O D ^ + B O D ^ = A O B ^ .
⇒ A O D ^ = A O B ^ − B O D ^ = m ° − 90 ° (1)
Tia OC nằm trong góc AOB nên A O C ^ + B O C ^ = A O B ^
⇒ B O C ^ = A O B ^ − A O C ^ = m ° − 90 ° (2)
Từ (1) và (2), suy ra: A O D ^ = B O C ^ = m ° − 90 °
b) Tia OC nằm giữa hai tia OB và OD. Suy ra B O C ^ + D O C ^ = B O D ^ = 90 ° .
Nếu B O C ^ = D O C ^ thì D O C ^ = 90 ° : 2 = 45 ° .
Do đó A O D ^ = D O C ^ = C O D ^ ⇔ A O B ^ = 3. D O C ^ = 3.45 ° = 135 ° ⇔ m = 135 .
Chứng tỏ hai đường thẳng vuông góc
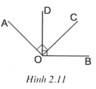

a) Vì tia OD nằm trong A O B ^ nên tia OD nằm giữa hai tia OA và OB do đó
A O D ^ + B O D ^ = A O B ^
Suy ra: A O D ^ = A O B ^ − B O D ^ = 90 0 − 60 0 = 30 0
Tương tự ta cũng có C O B ^ = 30 0 , D O C ^ = 30 0 .
b) Vì là tia phân giác của D O E ^ nên D O B ^ = B O E ^ = 60 0 .
Vì OB nằm giữa hai tia OC và OE và C O B ^ = 30 0 nên ta có
E O C ^ = E O B ^ + B O C ^ = 60 0 + 30 0 = 90 0
Vậy O C ⊥ O E
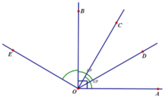

a) Vì O C ⊥ O A nên A O C ^ = 90 0 do đó A O D ^ + D O C ^ = A O C ^ suy ra A O D ^ = A O B ^ − B O D ^ = A O B ^ − 90 0 (1)
Vì O D ⊥ O B nên B O D ^ = 90 0 do đó B O C ^ + C O D ^ = B O D ^ suy ra B O C ^ = A O B ^ − A O C ^ = A O B ^ − 90 0 (2)
Từ (1) và (2) ta có B O C ^ = A O D ^ .
b) Vì tia OM là tia phân giác của A O B ^ nên A O M ^ = M O B ^ = 1 2 A O B ^ .
Mà C O M ^ + M O A ^ = 90 0 ( do A O C ^ = 90 0 );
D O M ^ + M O B ^ = 90 0 ( do B O D ^ = 90 0 ).
Vậy C O M ^ = D O M ^ ( cùng phụ với hai góc bằng nhau). (3)
Vì OM nằm giữa hai tia OC và OD và C O M ^ = D O M ^ (theo (3)) nên OM có phải là tia phân giác của D O C ^ .

Ta có:
Góc BOD + góc DOC = 1200
=> góc DOC = 1200 - góc BOD = 120o - 90o = 30o
Góc AOC + góc COB = 120o
=> góc COB = 120o - góc AOC= 120o - 90o = 300
mà Góc BOC + góc COD + góc DOA = 120o
=> góc COD = 120o - ( góc BOC + góc DOA) = 1200 - 600 = 600
Ta có:
Góc BOC = Góc AOD
=> 1 / 2 BOC = 1 / 2 OD= 30 / 2 =15o
hay góc nOC = góc mOD = 15o
mà góc nOm= góc nOC +góc mOD + góc COD = 15o +150 +600 = 90o
hay nO vuông góc với mO.

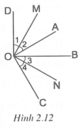
Ta có O C ⊥ O A ⇒ A O C ^ = 90 ° . O D ⊥ O B ⇒ B O D ^ = 90 ° .
Tia OB nằm giữa hai tia OA, OC.
Do đó A O B ^ + B O C ^ = 90 ° . (1)
Tương tự, ta có A O B ^ + A O D ^ = 90 ° . (2)
Từ (1) và (2) ⇒ B O C ^ = A O D ^ (cùng phụ với A O B ^ ).
Tia OM là tia phân giác của góc AOD ⇒ O 1 ^ = O 2 ^ = A O D ^ 2 .
Tia ON là tia phân giác của góc BOC ⇒ O 3 ^ = O 4 ^ = B O C ^ 2 .
Vì A O D ^ = B O C ^ nên O 1 ^ = O 2 ^ = O 3 ^ = O 4 ^ .
Ta có A O B ^ + B O C ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 4 ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 2 ^ = 90 ° .
Do đó M O N ^ = 90 ° ⇒ O M ⊥ O N


a. Ta có:
O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °
⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )
b. Ta có:
A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °
Mà A O D ^ + C O D ^ = 90 ° ( C M T )
40 ° + C O D ^ = 90 ° C O D ^ = 50 °
c. OM là tia phân giác của A O B ^ nên:
A O M ^ = B O M ^ = A O B ^ 2 = 65 °
A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °
Tương tự ta tìm được C O M ^ = 25 °
Do đó C O M ^ = D O M ^ ( = 25 ° )
Vậy OM là tia phân giác của C O D ^