Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
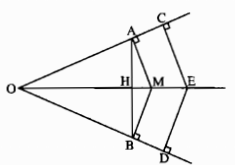
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.

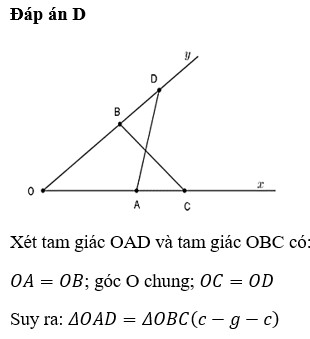
a/ Xét t/g OAD và t/g OBC cos
AO = OB
\(\widehat{xOy}\) : chung
OD = OC
=> t/g OAD = t/g OBC
=> AD = BC
b/ Không rõ đề.
c/ Có
OC = ODOA = OB
=> AC = BD
Có \(\widehat{OAD}=\widehat{OBE}\) (do t/g OAD = t/g OBC)
=> \(180^o-\widehat{OAD}=180^o-\widehat{OBE}\)
=> \(\widehat{CAD}=\widehat{CBD}\)
Xét t/g AEC và t/g BED có
\(\widehat{CAD}=\widehat{CBD}\)
AC = BD\(\widehat{OCB}=\widehat{ODA}\)
=> t/g AEC = t/g BED (g.c.g)
=> AE = BE
Xét t/g OAE và t/g OBE có
OA = OB
AE = BEOE : chung
=> t/g OAE = t/g OBE
=> ^xOE = ^yOe
=> OE là pg góc xOy

a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.
a) Ta có O C ⊥ O A nên A O C ^ = 90 ° ; O D ⊥ O B nên B O D ^ = 90 ° .
Tia OD nằm trong góc AOB nên A O D ^ + B O D ^ = A O B ^ .
⇒ A O D ^ = A O B ^ − B O D ^ = m ° − 90 ° (1)
Tia OC nằm trong góc AOB nên A O C ^ + B O C ^ = A O B ^
⇒ B O C ^ = A O B ^ − A O C ^ = m ° − 90 ° (2)
Từ (1) và (2), suy ra: A O D ^ = B O C ^ = m ° − 90 °
b) Tia OC nằm giữa hai tia OB và OD. Suy ra B O C ^ + D O C ^ = B O D ^ = 90 ° .
Nếu B O C ^ = D O C ^ thì D O C ^ = 90 ° : 2 = 45 ° .
Do đó A O D ^ = D O C ^ = C O D ^ ⇔ A O B ^ = 3. D O C ^ = 3.45 ° = 135 ° ⇔ m = 135 .
Chứng tỏ hai đường thẳng vuông góc