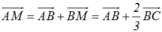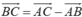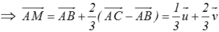Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm của BC
Vì ΔABC đều
mà M là trug điểm của bC
nên MA vuông góc với BC
BM=CM=a/2
\(AM=\sqrt{a^2-\left(\dfrac{1}{2}a\right)^2}=\dfrac{a\sqrt{3}}{2}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{BA}\right|=2\cdot AM=2\cdot\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)
\(\left|\overrightarrow{AB}-\overrightarrow{CA}\right|=\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}\)
vecto AB-vecto BC
=vecto AB+vecto CB
=>|vecto AB+vecto CB|=|vecto BA+vecto BC|=|2vecto BN|(Với N là trung điểm của AC)
=2xBN=a căn 3

\(\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AC}.\overrightarrow{BC}=12\)
\(\Leftrightarrow\overrightarrow{BC}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=12\)
\(\Leftrightarrow\overrightarrow{BC}.\overrightarrow{BC}=12\)
\(\Rightarrow BC^2=12\Rightarrow BC=2\sqrt{3}\)

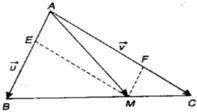
Ta có M B → = 1 3 M C → ⇔ 3 M B → = M C → ⇔ 3 B M → = C M →
A M → = A B → + B M → ⇒ 3 A M → = 3 A B → + 3 B M → ( 1 ) A M → = A C → + C M → ( 2 )
Lấy (1) trừ (2) ta được :
2 A M → = 3 A B → + 3 B M → − A C → + C M → = 3 A B → − A C → + ( 3 B M → − C M → ) = 3 A B → − A C → + 0 → = 3 A B → − A C → ⇒ A M → = 3 2 A B → − 1 2 A C → = 3 2 u → − 1 2 v →
Đáp án A

a: Gọi H là trung điểm của BC
Xét ΔABC có AH là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AH}\)
ΔABC đều có AH là đường trung tuyến
nên \(AH=AB\cdot\dfrac{\sqrt{3}}{2}=3a\cdot\dfrac{\sqrt{3}}{2}\)
=>\(2\cdot AH=3a\sqrt{3}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AH=3a\sqrt{3}\)
b:
Gọi I là trung điểm của AH
I là trung điểm của AH
=>\(IA=IH=\dfrac{3a\sqrt{3}}{2}\)
ΔABC đều
mà AH là đường trung tuyến
nên AH vuông góc BC
ΔIHC vuông tại H
=>\(CI^2=HI^2+HC^2\)
=>\(CI^2=\left(\dfrac{3a\sqrt{3}}{2}\right)^2+\left(1,5a\right)^2=9a^2\)
=>CI=3a
\(\left|\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(=\left|2\cdot\overrightarrow{CI}\right|=2CI\)
\(=2\cdot3a=6a\)