Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có :
\(BC^2=AB^2+AC^2\left(Pitago\right)\)
\(\Leftrightarrow AC^2=BC^2-AB^2=169-25=144\)
\(\Leftrightarrow AC=12\left(cm\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{AB^2.+AC^2}{AB^2.AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{BC^2}{\left(AB.AC\right)^2}\)
\(\Leftrightarrow AH^2=\dfrac{\left(AB.AC\right)^2}{BC^2}=\dfrac{\left(5.12\right)^2}{13^2}\)
\(\Leftrightarrow AH=\dfrac{5.12}{13}=\dfrac{60}{13}\sim4,85\left(cm\right)\)
\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13}\Rightarrow\widehat{B}\sim67^o\)
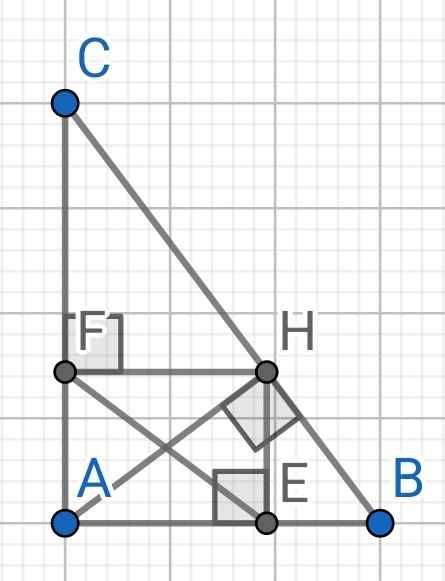 a) ∆ABC vuông tại A (gt)
a) ∆ABC vuông tại A (gt)
BC² = AB² + AC² (Pytago)A
⇒ AC² = BC² - AB²
= 13² - 5²
= 144
⇒ AC = 12 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5.12 : 13
= 60/13 (cm) ≈ 4,62 (cm)
sinB = AC/BC = 12/13
⇒ ∠B ≈ 67⁰
b) ∆AHB vuông tại H có HE là đường cao
⇒ HE² = AE . EB (1)
∆AHC vuông tại H có HF là đường cao
⇒ HF² = AF . FC (2)
Tứ giác AEHF có:
∠AEH = ∠EAF = ∠AFH = 90⁰
⇒ AEHF là hình chữ nhật
⇒ AH = EF
⇒ ∠EHF = 90⁰
∆EHF vuông tại H
⇒ EF² = HE² + HF²
⇒ AH² = HE² + HF²
Từ (1) và (2)
⇒ AE.EB + AF.FC = HE² + HF² = AH²
∆ABC vuông tại A vó AH là đường cao
⇒ AH² = HB.HC
⇒ AE.EB + AF.FC = HB.HC
⇒ AE.EB + AF.FC - HB.HC = 0
c) AH = EF đã chứng minh ở câu b

a, \(AB=\sqrt{BC^2-AC^2}=10\sqrt{5}\left(cm\right)\)
\(\cos B=\dfrac{AC}{BC}=\dfrac{2}{3}\approx48^0\Rightarrow\widehat{B}\approx48^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx90^0-48^0=42^0\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{20\sqrt{5}}{30}\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{40}{3}\left(cm\right)\end{matrix}\right.\)

a:
ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>\(BC^2=25+64=89\)
=>\(BC=\sqrt{89}\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}=\dfrac{8}{5}\)
=>\(\widehat{B}\simeq58^0\)
=>\(\widehat{C}=32^0\)
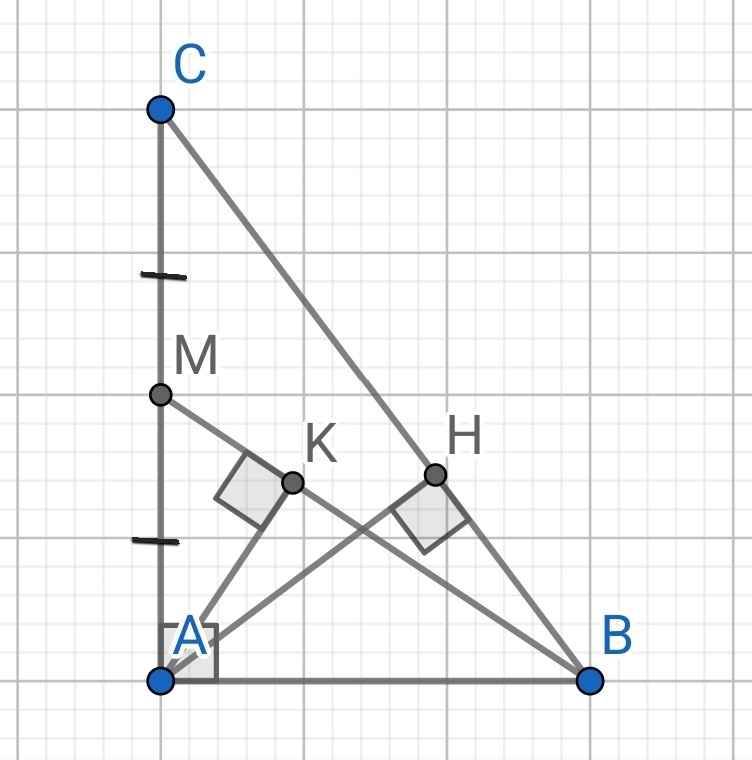
b: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
ΔAHB vuông tại H có HM vuông góc AB
nên AM*AB=AH^2; BM*BA=BH^2; AM*MB=HM^2
ΔAHC vuông tại H có HN làđường cao
nên AN*AC=AH^2;CN*CA=CH^2; NA*NC=NH^2
AM*MB+NA*NC
=HM^2+HN^2
=MN^2
c: AB^2/AC^2
\(=\dfrac{BH\cdot CB}{CH\cdot CB}=\dfrac{BH}{CH}\)

a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

2: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBDC vuông tại B có BA là đường cao ứng với cạnh huyền DC
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=4,8cm
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{ACB}\simeq36^052'\)
b: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF đồng dạng với ΔACB
=>\(\widehat{AFE}=\widehat{ABC}\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+12^2=20^2\)
=>\(AC^2=400-144=256\)
=>\(AC=\sqrt{256}=16\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>\(AH\cdot20=12\cdot16=192\)
=>AH=9,6(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{12^2}{20}=7,2\left(cm\right)\\CH=\dfrac{16^2}{20}=12,8\left(cm\right)\end{matrix}\right.\)
b: XétΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
c: \(AB\cdot cosB+AC\cdot cosC\)
\(=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=\dfrac{BC^2}{BC}=BC\)