MN
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
28 tháng 10 2021
Lời giải:
Áp dụng BĐT Cô-si:
$(a+b+c)(ab+bc+ac)\geq 9abc$
$\Rightarrow abc\leq \frac{1}{9}(a+b+c)(ab+bc+ac)$. Do đó:
$(a+b)(b+c)(c+a)=(ab+bc+ac)(a+b+c)-abc$
$\geq (ab+bc+ac)(a+b+c)-\frac{(ab+bc+ac)(a+b+c)}{9}=\frac{8}{9}(a+b+c)(ab+bc+ac)$
$\Rightarrow (a+b+c)(ab+bc+ac)\leq \frac{9}{8}(*)$
Mà cũng theo BĐT Cô-si:
$1=(a+b)(b+c)(c+a)\leq \left(\frac{a+b+b+c+c+a}{3}\right)^3$
$\Rightarrow a+b+c\geq \frac{3}{2}(**)$
Từ $(*); (**)\Rightarrow ab+bc+ac\leq \frac{9}{8}.\frac{1}{a+b+c}\leq \frac{9}{8}.\frac{2}{3}=\frac{3}{4}$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=\frac{1}{2}$
14 tháng 1 2023
a: Xét tứ giác AMBQ có
P là trung điểm chung của AB và MQ
MA=MB
=>AMBQ là hình thoi
b: BC=2*AM=20cm
\(AC=\sqrt{20^2-18^2}=\sqrt{76}=2\sqrt{19}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\sqrt{19}\cdot18=18\sqrt{19}\left(cm^2\right)\)
c: Để AMBQ là hình vuông thì góc ABM=45 độ
=>góc ABC=45 độ
d: \(MP=\dfrac{AC}{2}=\dfrac{2\sqrt{19}}{2}=\sqrt{19}\left(cm\right)\)
=>MQ=2 căn 19(cm)
\(S_{AMBQ}=\dfrac{1}{2}\cdot2\sqrt{19}\cdot18=18\sqrt{19}\left(cm^2\right)\)
18 tháng 9 2021
\(a,=\left(x+4\right)^3=\left(6+4\right)^3=10^3=1000\\ b,=x^3-1+x^3-27=2x^3-28\\ =2\left(-1\right)^3-28=-2-28=-30\\ c,=\left[4x-6-4\left(3-x\right)\right]\left[4x-64++4\left(3-x\right)\right]=6\left(8x-18\right)=12\left(4x-9\right)\\ =12\left(-7\cdot4-9\right)=12\left(-37\right)=-444\)
KK
26 tháng 8 2021
a. x2 - 2x
⇔ x(x - 2)
b. 3x - 6y
⇔ 3(x - 2y)
c. 5(x + 3y) - 15x(x + 3y)
⇔ (5 - 15x)(x + 3y)
d. 3(x - y) - 5x(y - x)
⇔ 3(x - y) + 5x(x - y)
⇔ (3 + 5x)(x - y)
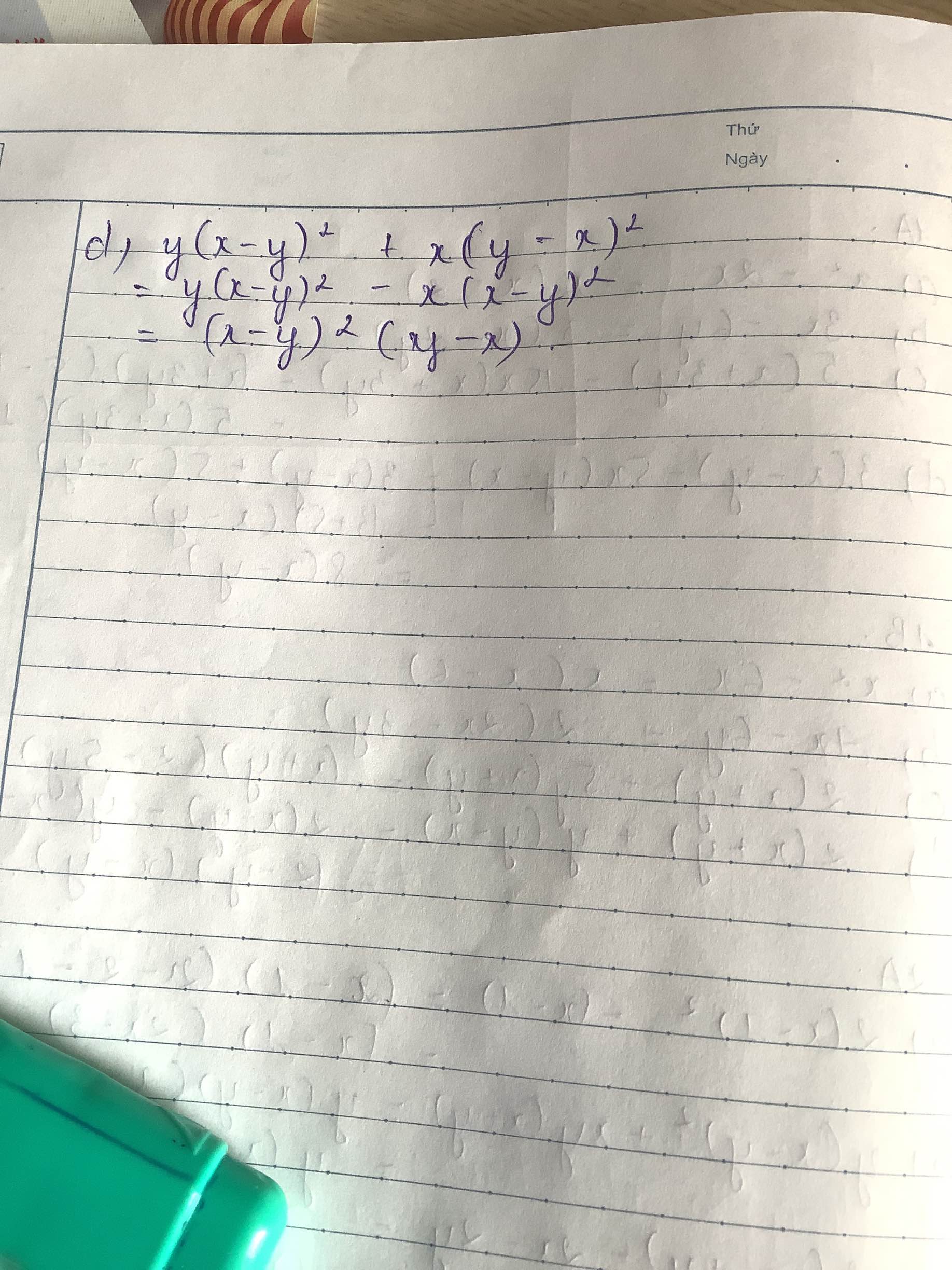
a^3+b^3+c^3=3abc thì a=b=c hay a+b+c=0 chứ sai đề r
a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)