Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Vì là tập tất cả các số tự nhiên có 5 chữ số nên
Số phần tử của không gian mẫu là 
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
có tận cùng bằng 1,do đó 
với 
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng
m
n
p
q
¯
Khi đó: 
- Với m = 1, do 
và q = 3 nên n
≥
4
+) Khi n = 4 thì p > 2 nên p ∈ {4;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi n ≥ 5: Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p ≠ m,n,q nên p có 7 cách chọn. Ta được 35 số thỏa mãn.
- Với m
≥
2 tức là có 7 cách chọn m từ tập {2;4;5;6;7;8;9}. Khi đó 
với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và n
≠
p
≠
m, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
2) M là số có 5 chữ số có dạng m n p q r ¯ Khi đó: m n p q r ¯ ≤ 14285 và r = 3
Do m n p q r ¯ ≤ 14285 nên m chỉ nhận giá trị bằng 1 và n ≤ 4
- Với m=1; n = 0,2 thì p,q là các số tùy ý thuộc tập {0;2;4;5;6;7;8;9} và p ≠ q ≠ n Ta được 2.7.6 = 84 số thỏa mãn.
- Với m=1; n = 4:
+) Khi p = 0 thì q là số tùy ý thuộc tập {2;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;5;6;7;8}. Ta được 5 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 6 + 35 + 392 + 84 + 6 + 5 = 528
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng
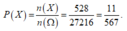
Chọn C
Ta có 
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà 
hoặc 
Vì 
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
Vậy xác suất cần tìm là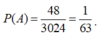 
Chọn A
Giả sử số cần lập là 
Số phần từ không gian mẫu: 
Gọi A là biến cố lấy được số chia hết cho 11 và tổng của các chữ số của chúng cũng chia hết cho 11.
Ta có:
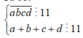
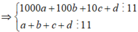
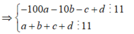
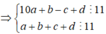
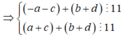
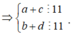
Từ 1,2,3,4,5,6,7,8,9 ta có 4 cặp tổng chia hết cho 11 là: 
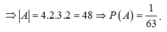
Chọn A
+ Ta có 
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà 
nên c có 3 cách chọn.
Ta có: 
Xác suất cần tìm là: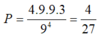 
Chọn A
Ta có tất cả các số tự nhiên có 5 chữ số bắt đầu từ 10000 đến 99999 gồm 90000 số.
Do đó n ( Ω ) = 90000
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 1.
Mà 90000 = 70x1285+50, nên ta chia 90000 số thành 1285 bộ 70 số liên tiếp và còn lại 50 số cuối, trong đó:
1285 bộ 70 số tự nhiên liên tiếp có 1285 số thỏa mãn yêu cầu
50 số cuối có 5 số tận cùng bằng 1 được xét trong bảng sau
| 99951 |
99961 |
99971 |
99981 |
99991 |
| Chia cho 7 dư 5 |
Chia cho 7 dư 1 |
Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 3 |
Vậy tất cả có 1286 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.
Gọi là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1’ thì n(A) = 1286
Suy ra 
Cách 2:
Vì A là tập tất cả các số tự nhiên có 5 chữ số nên
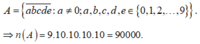
Số phần tử của không gian mẫu là 
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
Khi 
có tận cùng bằng 1, do đó 
với 
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng
m
n
p
q
¯
Khi đó: 
- Với m = 1, do 
+) Khi n = 4 thì p > 2 nên 
. Ta được 7 số thỏa mãn.
+) Khi n ≥ 5 : Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p được chọn tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 50 số thỏa mãn.
- Với m
≥
2 tức là có 8 cách chọn m từ tập {2;3;4;5;6;7;8;9}. Khi đó 
với mọi n,p thuộc tập hợp {0;1;2;3;4;5;6;7;8;9}. Ta được 8.10.10 = 800 số thỏa mãn.
2) M là số có 5 chữ số có dạng
m
n
p
q
r
¯
Khi đó: 
Do m n p q r ¯ ≤ 14285 nên m chỉ nhận giá trị bằng 1 và n ≤ 4
- Với m = 1; n = 0,1,2,3 thì p,q là các số tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 4.10.10 = 400 số thỏa mãn.
- Với m = 1; n = 4:
+) Khi p = 0 hoặc p = 1 thì q là số tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 2.10 = 20 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;1;2;3;4;5;6;7;8}. Ta được 9 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 7 + 50 + 8000 + 429 = 1286
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng
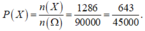
Đáp án A.
Gọi số cần tìm có dạng a b c d vì chia hết cho 6
⇒ d = { 2 , 4 , 6 , 8 } a + b + c + d : 3
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1 → 9).
+) Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .
Chọn A
Số phần tử của A là A 9 4 = 3024 số.
Số phần tử của không gian mẫu là n ( Ω ) = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng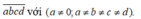
Theo bài ra ta có: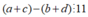
và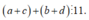 
Suy ra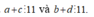
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là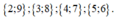
Chọn 2 cặp trong 4 cặp số trên để tạo số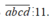
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48