Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Bạn tự vẽ
b, PT hoành độ giao điểm (d1) và (d3) là
\(x=-x+3\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow y=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};\dfrac{3}{2}\right)\Leftrightarrow OA=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(\dfrac{3}{2}-0\right)^2}=\dfrac{3\sqrt{2}}{2}\)
PT hoành độ giao điểm (d2) và (d3) là
\(2x=-x+3\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow B\left(1;2\right)\Leftrightarrow OB=\sqrt{\left(1-0\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
Ta có \(AB=\sqrt{\left(\dfrac{3}{2}-1\right)^2+\left(\dfrac{3}{2}-2\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\dfrac{\sqrt{2}}{2}\)
Ta có \(OA^2+AB^2=\dfrac{9}{2}+\dfrac{1}{2}=\dfrac{10}{2}=5=OB^2\) nên tg OAB vuông tại A
Do đó \(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot AB=\dfrac{1}{2}\cdot\dfrac{3\sqrt{2}}{2}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{3}{4}\left(đvdt\right)\)

a: (d1) và (d2) cắt nhau khi \(a-1\ne3-a\)
=>\(2a\ne4\)
=>\(a\ne2\)
(d1)//(d2) khi \(\left\{{}\begin{matrix}a-1=3-a\\2< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=4\\2< >1\left(đúng\right)\end{matrix}\right.\)
=>2a=4
=>a=2
Vì \(b_1=2\ne1=b_2\)
nên (d1) và (d2) không thể trùng nhau
b: Khi hai đường thẳng cắt nhau thì phương trình hoành độ giao điểm là:
\(\left(a-1\right)x+2=\left(3-a\right)x+1\)
=>\(\left(a-1-3+a\right)x=-1\)
=>\(\left(2a-4\right)x=-1\)
=>\(x=-\dfrac{1}{2a-4}\)
Khi \(x=-\dfrac{1}{2a-4}\) thì \(y=\left(a-1\right)\cdot\dfrac{-1}{2a-4}+2\)
\(=\dfrac{-a+1}{2a-4}+2\)
\(=\dfrac{-a+1+2\left(2a-4\right)}{2a-4}=\dfrac{3a-7}{2a-4}\)
vậy: Tọa độ giao điểm là \(A\left(-\dfrac{1}{2a-4};\dfrac{3a-7}{2a-4}\right)\)

Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m-2\ne-2\\m^2+5m+6=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne0\\m^2+5m=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\left(m+5\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne0\\\left[{}\begin{matrix}m=0\\m+5=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m+5=0\)
=>m=-5

1: \(O_2D=O_2A+CD=\dfrac{AC}{2}+\dfrac{BC}{2}=\dfrac{AB}{2}=R_1\)
góc O2MD=góc O2MC+góc CMD
=1/2*sđ cung CM+góc MCA
=90 độ
=>DM là tiếp tuyến của (O2)
PD^2=BD*DA=DC*BA=DM^2=O2D-R2^2
=>PD^2=R1^2-R2^2
2: Xet ΔD1BD vuông tại D1 và ΔD4BD vuông tại D4 có
BD chung
góc D1BD=góc D4BD
=>ΔD1BD=ΔD4BD
=>D1=D4
CM tương tự, ta được: DD2=DD3, BP=BQ, PA=PB
=>D1D+D2D+D3D+D4D<=1/2(BP+PA+AQ+QB)
=>2*(D1D+D2D)<=PA+PB
PB^2=BD^2+DP^2>=2*DB*DP
=>\(PB>=\dfrac{2\cdot DB\cdot DP}{PB}=2\cdot D_1D\)
Chứng minh tương tự,ta được: \(AP>=\dfrac{2\cdot DA\cdot DP}{PA}=2\cdot D_2D\)
=>ĐPCM

a: Để hai đường song song thì
\(\left\{{}\begin{matrix}2m^2-m=1\\m^2+m< >2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(2m+1\right)=0\\\left(m+2\right)\left(m-1\right)< >0\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
b: Thay x=2 vào (d1), ta đc:
\(y=2+2=4\)
Vì (d3) vuông góc với (d1) nên (d3): y=-x+b
Thay x=2 và y=4 vào (d3), ta được:
b-2=4
=>b=6

a: Tọa độ A là: x=4 và y=x=4
Tọa độ B là 3x=4 và y=4
=>x=4/3 và y=4
b: \(OA=\sqrt{\left(4-0\right)^2+\left(4-0\right)^2}=4\sqrt{2}\)
\(OB=\sqrt{\left(\dfrac{4}{3}\right)^2+4^2}=\dfrac{4\sqrt{10}}{3}\left(cm\right)\)
\(AB=\sqrt{\left(\dfrac{4}{3}-4\right)^2+\left(4-4\right)^2}=\dfrac{8}{3}\left(cm\right)\)
=>\(p=\dfrac{1}{2}\left(4\sqrt{2}+\dfrac{4}{3}\sqrt{10}+\dfrac{8}{3}\right)=2\sqrt{2}+\dfrac{2}{3}\sqrt{10}+\dfrac{4}{3}\left(cm\right)\)
=>S=16/3

a/ Hoành độ giao điểm của (d1) và (d3) là nghiệm của phương trình:
x = 4 => y = 4
Vậy tọa độ giao điểm A của (d1) và (d3) là A(4 ; 4)
Hoành độ giao điểm của (d2) và (d3) là nghiệm của phương trình:
3x = 4 <=> x = 4/3 => y = 4
Vậy tọa độ giao điểm B của (d2) và (d3) là B(4/3; 4)
b/ độ dài đt : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\dfrac{4}{3}-4\right)^2+\left(4-4\right)^2}=\dfrac{8}{3}\left(cm\right)\)
Gọi OH là đường cao của tam giác OAB và OH cũng chính là đt d3 :
\(S_{OAB}=\dfrac{1}{2}.\dfrac{8}{3}.4=\dfrac{16}{3}\left(cm^2\right)\)
Vậy ...
a/ Hoành độ giao điểm của (d1) và (d2) là nghiệm của phương trình:
x = 4 => y = 4
Vậy tọa độ giao điểm A của (d1) và (d2) là E(4 ; 4)
Hoành độ giao điểm của (d2) và (d3) là nghiệm của phương trình:
3x = 4 <=> x = 4/3 => y = 4
Vậy tọa độ giao điểm A của (d1) và (d2) là E(4/3; 4)
b/ điểm B ????
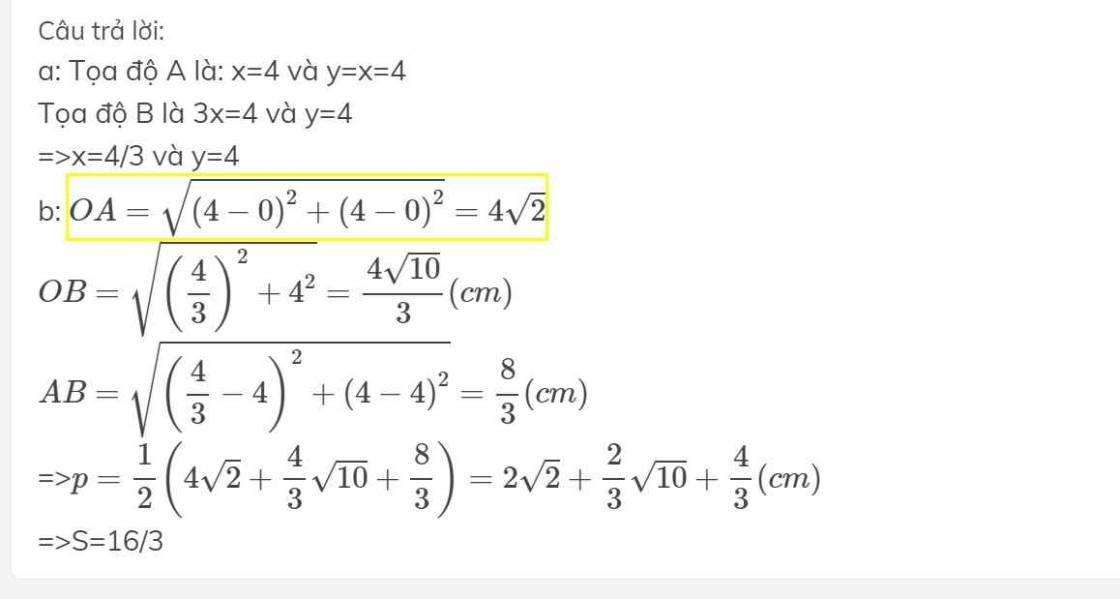
b: Vì (d1)//(d3) nên a=1
hay (d1): y=x+b
Thay x=2 và y=3 vào (d1), ta được:
b+2=3
hay b=1