Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì △ A'B'C' đồng dạng △ ABC theo tỉ số k nên ta có:
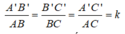
Theo tính chất dãy tỉ số bằng nhau, ta có:
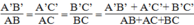
Suy ra: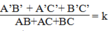 
Vậy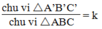 
Do 2 tam giác A'B'C' đồng dạng với tam giác ABC nên 2 tam giác này bằng nhau
=> A'B'=AB ; B'C'=BC ; A'C'=AC
Nên A'B'+B'C'+A'C'=AB+AC+BC ( theo công thức tính chu vi tam giác)
Nên chu vi 2 tam giác trên bằng nhau
tam giác ABC đồng dạng tam giác A'B'C'
=> \(\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}=k\)
áp dụng tính chất day tỉ số bằng nhau có:
\(\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}=\frac{AB+BC+AC}{A'B'+B'C'+A'C'}=k\)
=> \(\frac{Chuvi_{\Delta ABC}}{Chuvi_{\Delta}A'B'C}=k\) (đpcm)
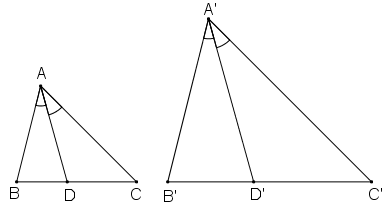
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
( Bạn tự kẻ hình nhé!!! )
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'
Tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k nên:
\(\widehat{B'}=\widehat{B}\), \(\widehat{A'}=\widehat{A}\), \(\frac{A'B'}{AB}=k\)
Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
\(\widehat{B'A'D'}=\frac{1}{2}\widehat{B'A'C'}\), \(\widehat{BAD}=\frac{1}{2}\widehat{BAC}\)
\(\Rightarrow\widehat{B'A'D'}=\widehat{BAD}\)
Xét tam giác A'B'D' và tam giác ABD:
\(\widehat{B'}=\widehat{B}\)
\(\widehat{B'A'D'}=\widehat{BAD}\)
\(\Rightarrow\)tam giác A'B'D' đồng dạng với tam giác ABD
\(\Rightarrow\frac{A'D'}{AD}=\frac{A'B'}{AB}=k\)
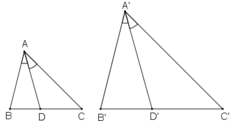
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
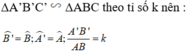
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
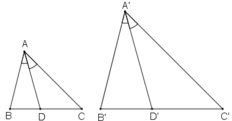
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
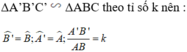
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
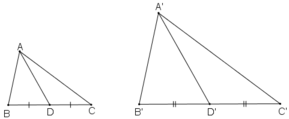
Giả sử ΔA’B’C’ 
ΔABC theo tỉ số k
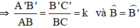
Gọi D, D’ lần lượt là trung điểm BC và B’C’
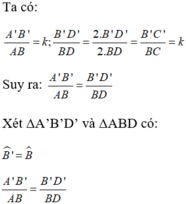
⇒ ΔA’B’D’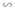 
ΔABD theo tỉ số k.
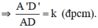
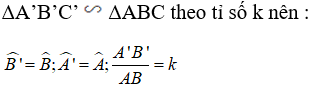
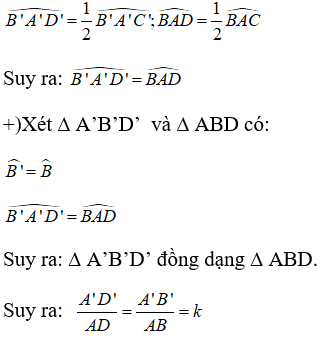
nịt