Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H(2;2) M E K(3;1) d :x+y-6=0 2 d :2x-y-2=0 1
Ta thấy ^EHK = ^EHM + ^KHM = ^BAE + ^CAM = ^BAC = 900
Đường thẳng HE: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HK}\left(1;-1\right)\Rightarrow\) \(HE:x-y=0\)
Xét hệ \(\hept{\begin{cases}x-y=0\\x+y-6=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\\y=3\end{cases}}}\Rightarrow E\left(3;3\right)\)
Đường thẳng KE: đi qua \(K\left(3;1\right)\), VTCP \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KE:\hept{\begin{cases}x=3\\y=1+2t\end{cases}}\)
Xét hệ \(\hept{\begin{cases}2x-y-2=0\\x=3\\y=1+2t\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=4\end{cases}}\Rightarrow A\left(3;4\right)\)
Đường thẳng BC: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HA}\left(1;2\right)\Rightarrow BC:x+2y-6=0\)(1)
Đường thẳng EB: đi qua \(E\left(3;3\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow BE:y=3\)(2)
Đường thẳng KC: đi qua \(K\left(3;1\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KC:y=1\) (3)
Từ (1);(2) suy ra \(B\left(0;3\right)\), từ (1);(3) suy ra \(C\left(4;1\right)\)
Vậy \(A\left(3;4\right),B\left(0;3\right),C\left(4;1\right).\)

Lời giải:
Phép tịnh tiến qua vecto $v$ biến $(d_3)$ thành chính nó thì $\overrightarrow{v}$ vecto chỉ phương của $(d_3)$
$\Rightarrow \overrightarrow{v}=(a,0)$
$T_{\overrightarrow{v}}(d_1)=d_2$
\(\Rightarrow \left\{\begin{matrix} 2x-y+2=0\\ 2(x+a)-y+1=0\end{matrix}\right.\Rightarrow a=\frac{1}{2}\)
Vậy $\overrightarrow{v}=(\frac{1}{2}, 0)$

\(d_2\) vuông góc \(d_1\) nên nhận (1;2) là 1 vtpt
d' là ảnh của \(d_2\) qua phép tịnh tiến \(\Rightarrow d'\) cùng phương \(d_2\Rightarrow d'\) cũng nhận (1;2) là 1 vtpt, pt d' có dạng:
\(x+2y+c=0\) (1)
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
\(\left\{{}\begin{matrix}x'=-1+4=3\\y'=2+\left(-3\right)=-1\end{matrix}\right.\) \(\Rightarrow A'\left(3;-1\right)\)
Thế vào (1):
\(3+2.\left(-1\right)+c=0\Rightarrow c=-1\)
Vậy pt d' là: \(x+2y-1=0\)

Đáp án D
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2 .

Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có ![]() tam giác.
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có ![]() tam giác.
tam giác.
Theo bài ra ta có: ![]()
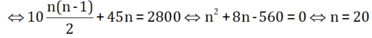
Chọn A.
Gọi \(A_1\) và \(A_2\) lần lượt là điểm đối xứng A qua \(d_1\) và \(d_2\Rightarrow\left\{{}\begin{matrix}A_1\left(4;3\right)\\A_2\left(\frac{7}{5};\frac{24}{5}\right)\end{matrix}\right.\)
Với B bất kì thuộc d1 và C bất kì thuộc d2, ta luôn có \(\left\{{}\begin{matrix}AB=A_1B\\AC=A_2C\end{matrix}\right.\)
\(\Rightarrow T=AB+BC+AC=A_1B+BC+CA_2\ge A_1A_2\)
\(\Rightarrow T_{min}=A_1A_2\) khi \(A_1;B;C;A_2\) thẳng hàng hay B, C lần lượt là giao điểm của đường thẳng \(A_1A_2\) và d1; d2
\(\overrightarrow{A_1A_2}=\left(-\frac{13}{5};\frac{9}{5}\right)\Rightarrow A_1A_2\) có 1 vtpt là \(\left(9;13\right)\)
Phương trình A1A2:
\(9\left(x-4\right)+13\left(y-3\right)=0\Leftrightarrow9x+13y-75=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}y=x\\9x+13y-75=0\end{matrix}\right.\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}y=2x\\9x+13y-75=0\end{matrix}\right.\)