
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



g) \(\left(4^{2x}-1\right)^2=5^2.9\)
\(\Leftrightarrow\left[{}\begin{matrix}4^{2x}-1=5.3\\4^{2x}-1=-5.3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4^{2x}=16\\4^{2x}=-14\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow4^{2x}=4^2\)
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
h) \(2^{x+1}+2^{x+2}+2^{x+3}+...+2^{x+101}=2^{104}-8\)
\(\Leftrightarrow2^{x+1}\left(1+2+2^2+...+2^{100}\right)=2^{104}-8\)
\(\Leftrightarrow2^{x+1}.\left(2^{101}-1\right)=2^{104}-2^3\)
\(\Leftrightarrow2^{x+1}=\dfrac{2^{104}-2^3}{2^{101}-1}\)
\(\Leftrightarrow2^{x+1}=\dfrac{2^3\left(2^{101}-1\right)}{2^{101}-1}\)
\(\)\(\Leftrightarrow2^{x+1}=2^3\)
\(\Leftrightarrow x+1=3\)
\(\Leftrightarrow x=2\)

Bài 6:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{41}=\dfrac{b}{29}=\dfrac{c}{30}=\dfrac{a+b}{41+29}=\dfrac{700}{70}=10\)
Do đó: a=410; b=290; c=300

\(\frac{13}{7}-\frac{8}{6}+\frac{8}{7}-\frac{4}{6}-\frac{1}{3}\)
\(=\left(\frac{13}{7}+\frac{8}{7}\right)-\left(\frac{8}{6}+\frac{4}{6}\right)-\frac{1}{3}\)
\(=3-2-\frac{1}{3}\)
\(=1-\frac{1}{3}\)
\(=\frac{2}{3}\)
Ta có \(\frac{13}{7}-\frac{8}{6}+\frac{8}{7}-\frac{4}{6}-\frac{1}{3}\)
\(=\frac{13}{7}-\frac{8}{6}+\frac{8}{7}-\frac{4}{6}-\frac{2}{6}\)
\(=\left(\frac{13}{7}+\frac{8}{7}\right)-\left(\frac{8}{6}+\frac{4}{6}+\frac{2}{6}\right)\)
\(=3-2\)
\(=1\)

Ta có:
∠A₁ + ∠A₂ = 180⁰ (kề bù)
⇒ ∠A₂ = 180⁰ - ∠A₁ (1)
Lại có:
∠A₁ + ∠B₁ = 180⁰
⇒ ∠B₁ = 180⁰ - ∠A₁ (2)
Từ (1) và (2) ⇒ ∠A₂ = ∠B₁
Mà ∠A₂ và ∠B₁ là hai góc so le trong
⇒ a // b
4:
\(\widehat{A_1}=\widehat{A_3}\)(đối đỉnh)
\(\widehat{A_1}+\widehat{B_1}=180^0\)
=>\(\widehat{A_3}+\widehat{B_1}=180^0\)
mà hai góc này ở vị trí trong cùng phía
nên a//b

OM\(\perp\)AB
=>\(\widehat{MOA}=\widehat{MOB}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOE}< \widehat{AOM}\)
nên tia OE nằm giữa hai tia OA và OM
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{AOM}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OB, ta có: \(\widehat{BOF}< \widehat{BOM}\)
nên tia OF nằm giữa hai tia OB và OM
=>\(\widehat{BOF}+\widehat{MOF}=\widehat{BOM}=90^0\)
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{BOF}+\widehat{MOF}\)
mà \(\widehat{AOE}=\widehat{BOF}\)
nên \(\widehat{MOE}=\widehat{MOF}\)
=>OM là phân giác của \(\widehat{EOF}\)


Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\)
Do đó: a=30; b=40; c=50


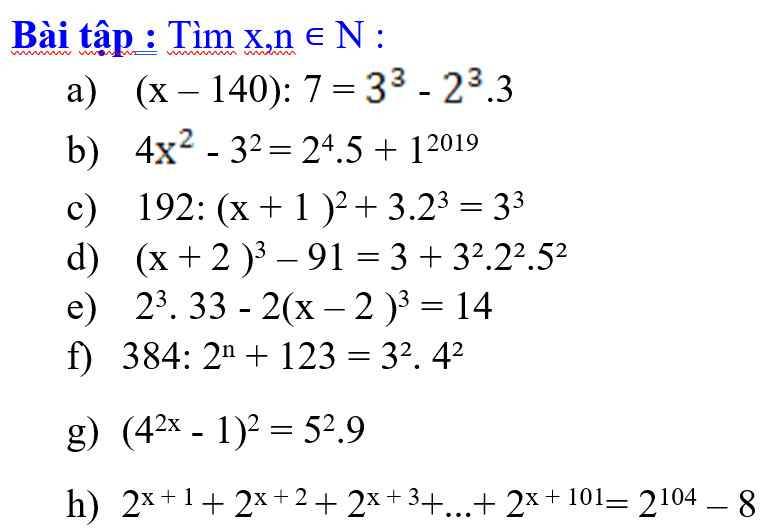

 mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17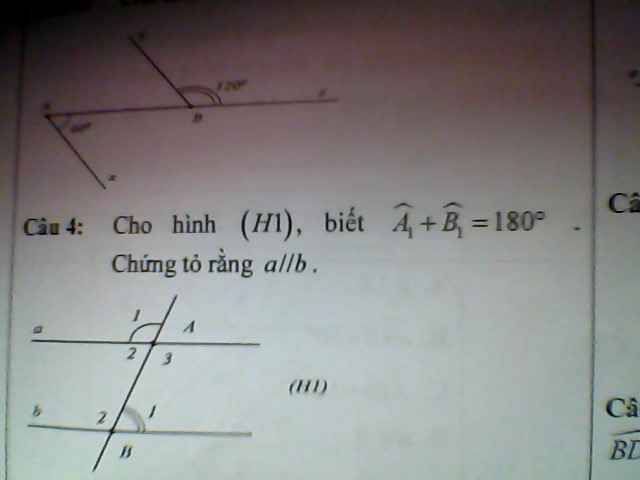



Bài 6:
a:
Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAC}\)
b: Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
\(\widehat{KAD}=\widehat{HAD}\)
Do đó: ΔAKD=ΔAHD
Suy ra: AK=AH