Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(5\sqrt{16}-4\sqrt{9}+\sqrt{25}-0,3\sqrt{400}\)
\(=20-12+5-6\)
\(=7\)
Ý của bạn là \(\left(5\sqrt{16}\right)-\left(4\sqrt{9}\right)+\left(\sqrt{25}\right)-\left(0,3\sqrt{400}\right)\)phải k???
\(\left(5\sqrt{16}\right)-\left(4\sqrt{9}\right)+\left(\sqrt{25}\right)-\left(0,3\sqrt{400}\right)\)
\(=\left(5.4\right)-\left(4.3\right)+5-\left(0,3.20\right)\\ =20-12+5-6\\ =8+5-6\\ =13-6\\ =7\)
Chúc các bạn học tốt ![]()




a) Ta có : \(x=\sqrt{40+2}=\sqrt{42}< \sqrt{49}=7\) (1)
\(y=\sqrt{40}+\sqrt{2}>\sqrt{36}+\sqrt{1}=6+1=7\) (2)
Từ (1) và (2) => x = y
b) Ta có : \(x=\sqrt{625}-\frac{1}{\sqrt{5}}=25-\frac{1}{\sqrt{5}}\) (1)
\(y=\sqrt{576}-\frac{1}{\sqrt{6}}+1=24-\frac{1}{\sqrt{6}}+1=25-\frac{1}{\sqrt{6}}\) (2)
Vì \(\sqrt{5}< \sqrt{6}\)nên \(\frac{1}{\sqrt{5}}>\frac{1}{\sqrt{6}}\)(3)
(1),(2),(3) => \(x>y\)


Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
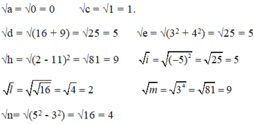
a: \(\dfrac{\sqrt{81}}{\sqrt{16}}=\dfrac{9}{4}=\dfrac{36}{16}< \dfrac{81}{16}\)
b: \(\sqrt{16+25}=\sqrt{41}< 9=\sqrt{16}+\sqrt{25}\)