Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay cặp số ( 1; 3) vào vế trái của bất phương trình ta được :
5.1 – 2( 3-1) >0
Do đó, cặp số (1 ;3) không là nghiệm của bất phương trình đã cho.
Chọn C

a: Thay x=-1 và y=2 vào 2x-y+3, ta được:
\(2x-y+3=-2-2+3=-1< 0\)
=>(-1;2) không là nghiệm của bất phương trình 2x-y+3>0
b:
-x+2+2(y-2)<2(2-x)(1)
=>-x+2+2y-4<4-2x
=>-x+2y-2-4+2x<0
=>x+2y-6<0
Thay x=-1 và y=2 vào x+2y-6, ta được:
\(x+2y-6=-1+4-6=-3< 0\)
=>(-1;2) là nghiệm của bất phương trình (1)
c: Thay x=-1 và y=2 vào x-y-15, ta được:
\(x-y-15=-1-2-15=-18< 0\)
=>(-1;2) là nghiệm của bất phương trình x-y-15<0
d: 3(x-1)+4(y-2)<5x-3(2)
=>3x-3+4y-8<5x-3
=>3x+4y-11-5x+3<0
=>-2x+4y-8<0
=>x-2y+4>0
Khi x=-1 và y=2 thì \(x-2y+4=-1-4+4=-1< 0\)
=>(-1;2) không là nghiệm của bất phương trình (2)

Tham khảo:
a) Đường thẳng \(y = 2x + 1\) đi qua điểm \(A(0;1)\) và \(B\left( { - \frac{1}{2};0} \right)\)
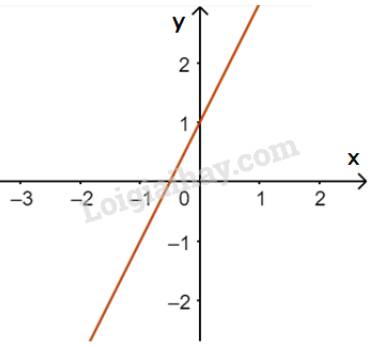
b)
Vì \(2.( - 2) - 0 + 1 = - 3 < 0\)nên \(( - 2;0)\) là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.0 - 0 + 1 = 1 > 0\)nên \((0;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.1 - 1 + 1 = 2 > 0\)nên \(( - 2;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

(1;1) không thuộc miền nghiệm vì 1+1=2>2 (Vô lý) => Loại A
(2;0) không thuộc miền nghiệm vì 2+0=2>2 (Vô lý) => Loại B
(3;2) thuộc miền nghiệm vì: 3+2 =5 > 2 (đúng) và \(3 - 2 = 1 \ge 1\) (đúng)
(3;-2) không thuộc miền nghiệm vì 3+ (-2)=1>2 (Vô lý) => Loại D
Chọn C.

1/ \(\Leftrightarrow\left(m-2\right)x^2+2x+m>0,\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\Delta'< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>2\\1-m\left(m-2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\m^2-2m-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>2\\\left[{}\begin{matrix}m>1+\sqrt{2}\\m< 1-\sqrt{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m>1+\sqrt{2}\)
2/ \(\overrightarrow{AB}=\left(-2;-4\right)\Rightarrow\overrightarrow{n_{AB}}=\left(4;-2\right)\)
\(\Rightarrow PTTS:\left\{{}\begin{matrix}x=3-2t\\y=7-4t\end{matrix}\right.\)
\(\Rightarrow PTTQ:4\left(x-3\right)-2\left(y-7\right)=0\)
\(4x-2y+2=0\)
b/ \(\Delta//AB\Rightarrow\overrightarrow{n_{\Delta}}=\overrightarrow{n_{AB}}=\left(4;-2\right)\)
\(\Rightarrow\Delta:4\left(x-1\right)-2y=0\)
\(:4x-2y-4=0\)
c/ \(\left(d\right)\perp\Delta\Rightarrow\overrightarrow{n_d}=\overrightarrow{u_{\Delta}}=\overrightarrow{AB}=\left(-2;-4\right)\)
\(\Rightarrow\left(d\right):-2x-4\left(y-1\right)=0\)
\(:-2x-4y+4=0\)

a) Vì \(4.9 - 7.1 - 28 = 1 \ge 0\)nên \((9;1)\) là nghiệm của bất phương trình \(4x - 7y - 28 \ge 0.\)
b) Vì \(4.2 - 7.6 - 28 = - 62 < 0\)nên \((2;6)\) không là nghiệm của bất phương trình \(4x - 7y - 28 \ge 0.\)
c) Vì \(4.0 - 7.( - 4) - 28 = 0 \ge 0\)nên \((0; - 4)\) là nghiệm của bất phương trình \(4x - 7y - 28 \ge 0.\)
Thay cặp số ( 1; 3) vào vế trái của bất phương trình ta được :
5.1 – 2( 3-1) >0
Do đó, cặp số (1 ;3) không là nghiệm của bất phương trình đã cho.