
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 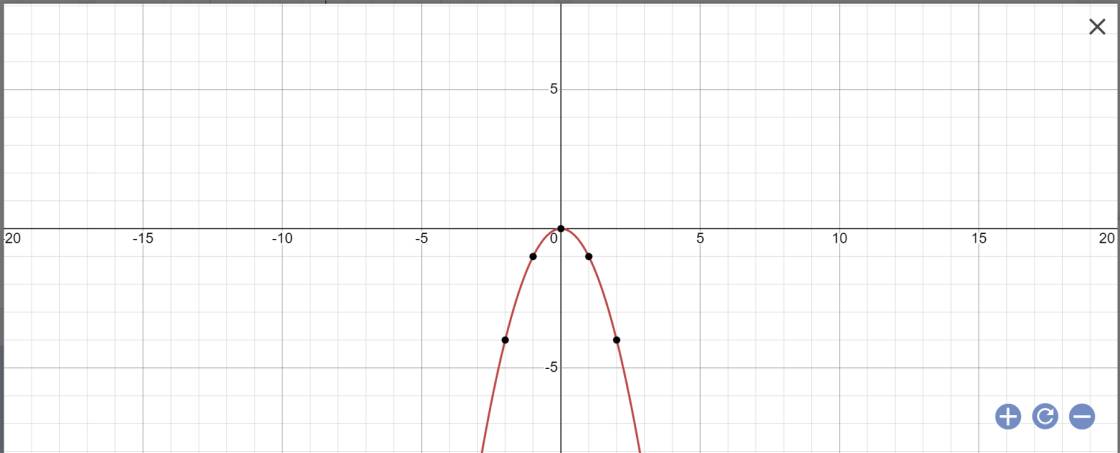
b: PTHĐGĐ là:
-x^2-2x+3m=0
=>x^2+2x-3m=0
Δ=(-2)^2-4*(-3m)=12m+4
Để (P) cắt (d) tại hai điểm pb thì 12m+4>0
=>m>-1/3
Sửa đề: x1.x2^2+x2.(3m-2x1)= 6
<=> x2.( x1.x2+3m-2x1) = 6
<=> x2.( -3m+3m-2x1) = 6
<=> -2x1x2 = 6
<=> x1.x2 =-3
<=> -3m =-3
<=> m=1

n: Ta có: \(\sqrt{2x+3}=1+\sqrt{2}\)
\(\Leftrightarrow2x+3=3+2\sqrt{2}\)
hay \(x=\sqrt{2}\)
q: Ta có: \(\sqrt{3x-2}=2-\sqrt{3}\)
\(\Leftrightarrow3x-2=7-4\sqrt{3}\)
\(\Leftrightarrow3x=9-4\sqrt{3}\)
hay \(x=\dfrac{9-4\sqrt{3}}{3}\)

b/ ĐKXĐ: \(x\ge2\)
P= \(\sqrt{x^2-4x+4}-4x+3\)
= \(\sqrt{\left(x-2\right)^2}-4x+3\)
= \(x-2-4x+3\)
= \(1-3x\)

Bài 2: Giải:
Ta có:
\(2a^2+a=3b^2+b\Leftrightarrow2a^2-2b^2+a-b=b^2\)
\(\Leftrightarrow\left(a-b\right)\left(2a+b+1\right)=b^2\left(1\right)\)
Đặt \(ƯCLN\left(a-b;2a+2b+1\right)=d\)
\(\Rightarrow\) \(\begin{cases}a-b\vdots d\\2a+2b+1\vdots d\end{cases}\) \(\Rightarrow b^2=\left(a-b\right)\left(2a+2b+1\right)⋮d^2\)
\(\Rightarrow b⋮d.\) Lại có: \(2\left(a-b\right)-\left(2a+2b+1\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\Rightarrow\left(a-b;2a+2b+1\right)=1\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) \(\Rightarrow\) Đpcm


22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)

Bài 1:
a: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔABC có
O là trung điểm của AB
H là trung điểm của BC
Do đó: OH là đường trung bình của ΔABC
Suy ra: OH//AC
hay OH\(\perp\)CB
Suy ra: ΔOHB vuông tại H

\(\frac{4x}{1-x^2}=\sqrt{5}\) ĐKXĐ : x khác 1
\(\Rightarrow4x=\sqrt{5}\left(1-x^2\right)\)
\(\Leftrightarrow4x=\sqrt{5}-x^2\sqrt{5}\)
\(\Leftrightarrow x^2\sqrt{5}-4x-\sqrt{5}=0\)
\(\Leftrightarrow x^2\sqrt{5}-5x+x-\sqrt{5}=0\)
\(\Leftrightarrow x\sqrt{5}\left(x-\sqrt{5}\right)+\left(x-\sqrt{5}\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{5}\right)\left(x\sqrt{5}+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-\sqrt{5}=0\\x\sqrt{5}=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{5}\left(tmđk\right)\\x=-\frac{1}{\sqrt{5}}=-\frac{\sqrt{5}}{5}\left(tmđk\right)\end{cases}}}\)
\(4x=\sqrt{5}-\sqrt{5}x^2\)
\(\Rightarrow4x+\sqrt{5}x^2=\sqrt{5}\)
\(\Rightarrow x\left(4+\sqrt{5}x\right)=\sqrt{5}\)
\(\Rightarrow x.\sqrt{5}\left(\frac{4}{\sqrt{5}}+x\right)=\sqrt{5}\)
\(\Rightarrow x.\left(\frac{4}{\sqrt{5}}+x\right)=1\)
Với x = 1 \(\Rightarrow\frac{4}{\sqrt{5}}+x=1\Rightarrow x=1-\frac{4}{\sqrt{5}}=\frac{5-4\sqrt{5}}{5}\)
Với x = -1\(\Rightarrow\frac{4}{\sqrt{5}}+x=-1\Rightarrow x=-1-\frac{4}{\sqrt{5}}=-\frac{5+4\sqrt{5}}{5}\)
ko có x thỏa mãn

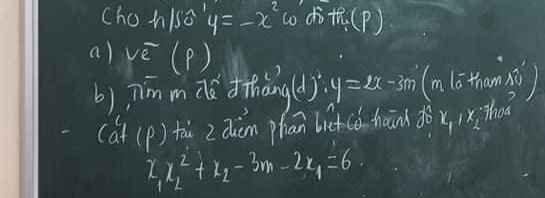





Bài 27:
a. $4=2.2=2.\sqrt{4}>2.\sqrt{3}$
b. $-\sqrt{5}< -\sqrt{4}=-2$
Bài 28:
a.
\((\sqrt{2}+\sqrt{3})^2=5+2\sqrt{6}=5+2\sqrt{\frac{24}{4}}< 5+2\sqrt{\frac{25}{4}}=5+2.\frac{5}{2}=10\)
$\Rightarrow \sqrt{2}+\sqrt{3}< \sqrt{10}$
b.
\((\sqrt{3}+2)^2=7+4\sqrt{3}\)
\((\sqrt{2}+\sqrt{6})^2=8+4\sqrt{3}\)
Mà $7+4\sqrt{3}< 8+4\sqrt{3}$
$\Rightarrow (\sqrt{3}+2)^2< (\sqrt{2}+\sqrt{6})^2$
$\Rightarrow \sqrt{3}+2< \sqrt{2}+\sqrt{6}$
c.
$\sqrt{15}.\sqrt{17}=\sqrt{15.17}=\sqrt{(16-1)(16+1)}=\sqrt{16^2-1}$
$<\sqrt{16^2}=16$
d.
\((\sqrt{15}+\sqrt{17})^2=32+2\sqrt{15.17}< 32+2.16=64\) (theo kq phần c)
$\Rightarrow \sqrt{15}+\sqrt{17}< \sqrt{64}=8$