Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

a: EF=12cm
b: Xét ΔDEI vuông tại E và ΔDKI vuông tại K có
DI chung
\(\widehat{EDI}=\widehat{KDI}\)
Do đó:ΔDEI=ΔDKI
c: Ta có: ΔDEI=ΔDKI
nên DE=DK
hay ΔDEK cân tại D
d: ta có: ΔDEI=ΔDKI
nên IE=IK
mà DE=DK
nên DI là đường trung trực của EK

Ta có
3344=(3.11)44=344.1144=(34)11.1144=8111.1144
4433=(4.11)33=433.1133=(43)11.1133=6411.1133
=> 3344>4433
KL:
b) 52222=(52)1111=251111
25555=(25)1111=321111
=> 52222<25555
KL


Câu 2:
b: \(\Leftrightarrow2n-4+9⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(n\in\left\{3;1;5;-1;11;-7\right\}\)
Câu 1:
a: \(=\dfrac{3^{44}\cdot3^{17}}{3^{30}\cdot3^{13}}=3^{18}\)
b: \(=-2+\dfrac{1}{19-\dfrac{1}{2+1:\dfrac{3}{2}}}=-2+\dfrac{1}{19-\dfrac{3}{8}}\)
\(=-2+1:\dfrac{149}{8}=-2+\dfrac{8}{149}=-\dfrac{290}{149}\)

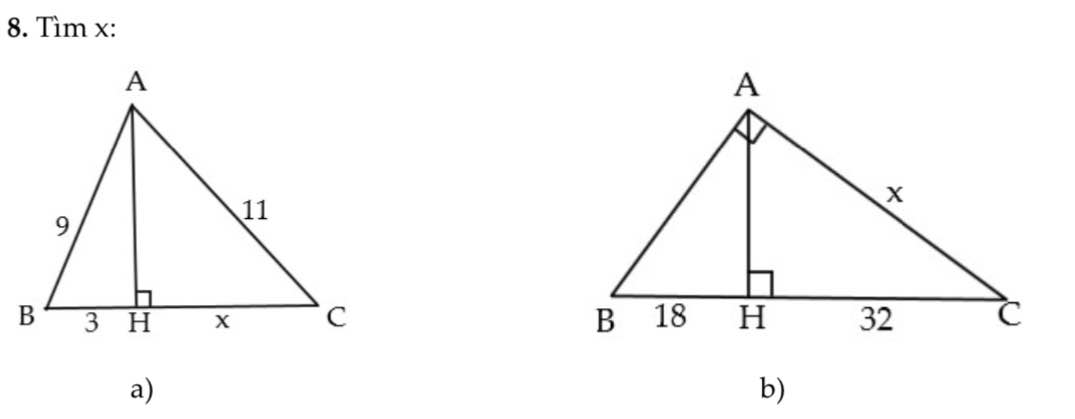
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
b: Xét ΔOEF có
OM là đường cao
OM là đường phân giác
Do đó: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của FE
hay FM=EM







C
C