K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2021
\(1,\\ a,x^4-8x^2-9=0\\ \Leftrightarrow x^4+x^2-9x^2-9=0\\ \Leftrightarrow\left(x^2+1\right)\left(x^2-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1=0\\x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\left(x^2+1\ge1>0\right)\\x=3\\x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\\ b,\left\{{}\begin{matrix}2\left(x-1\right)-3\left(x-3y\right)=5\\3\left(x-1\right)+5\left(x-3y\right)=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6\left(x-1\right)-9\left(x-3y\right)=15\\6\left(x-1\right)+10\left(x-3y\right)=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}19\left(x-3y\right)=-19\\3\left(x-1\right)+5\left(x-3y\right)=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-3y=-1\\3\left(x-1\right)-5=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3y=-1\\x-1=-\dfrac{7}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{3}\\-\dfrac{4}{3}-3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{3}\\y=-\dfrac{1}{9}\end{matrix}\right.\)
30 tháng 9 2021
5b.
Theo Bunhiacopxki:
\(\left(\sqrt{x\left(2x+y\right)}+\sqrt{y\left(2y+x\right)}\right)^2\le\left(x+y\right)\left(\left(2x+y\right)+\left(2y+x\right)\right)=3\left(x+y\right)^2\)
\(\Rightarrow\sqrt{x\left(2x+y\right)}+\sqrt{y\left(2y+x\right)}\le\sqrt{3}\left(x+y\right)\)
\(\Rightarrow\dfrac{x+y}{\sqrt{x\left(2x+y\right)}+\sqrt{y\left(2y+x\right)}}\ge\dfrac{x+y}{\sqrt{3}\left(x+y\right)}=\dfrac{1}{\sqrt{3}}\)
Dấu "=" xảy ra khi x=y
9 tháng 11 2021
Bài 1: hình 2:
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow20x=144\Rightarrow x=\dfrac{36}{5}\)
\(x+y=BC\Rightarrow\dfrac{36}{5}+y=20\Rightarrow y=\dfrac{64}{5}\)
Bài 2:
hình 4:
BC=BH+HC=1+4=5
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow1.5=AB^2\Rightarrow x=\sqrt{5}\)
áp dụng HTL ta có: \(HC.BC=AC^2\Rightarrow4.5=AC^2\Rightarrow y=2\sqrt{5}\)
hình 6:
Áp dụng HTL ta có: \(BH.HC=AH^2\Rightarrow4x=25\Rightarrow x=\dfrac{25}{4}\)
26 tháng 10 2021
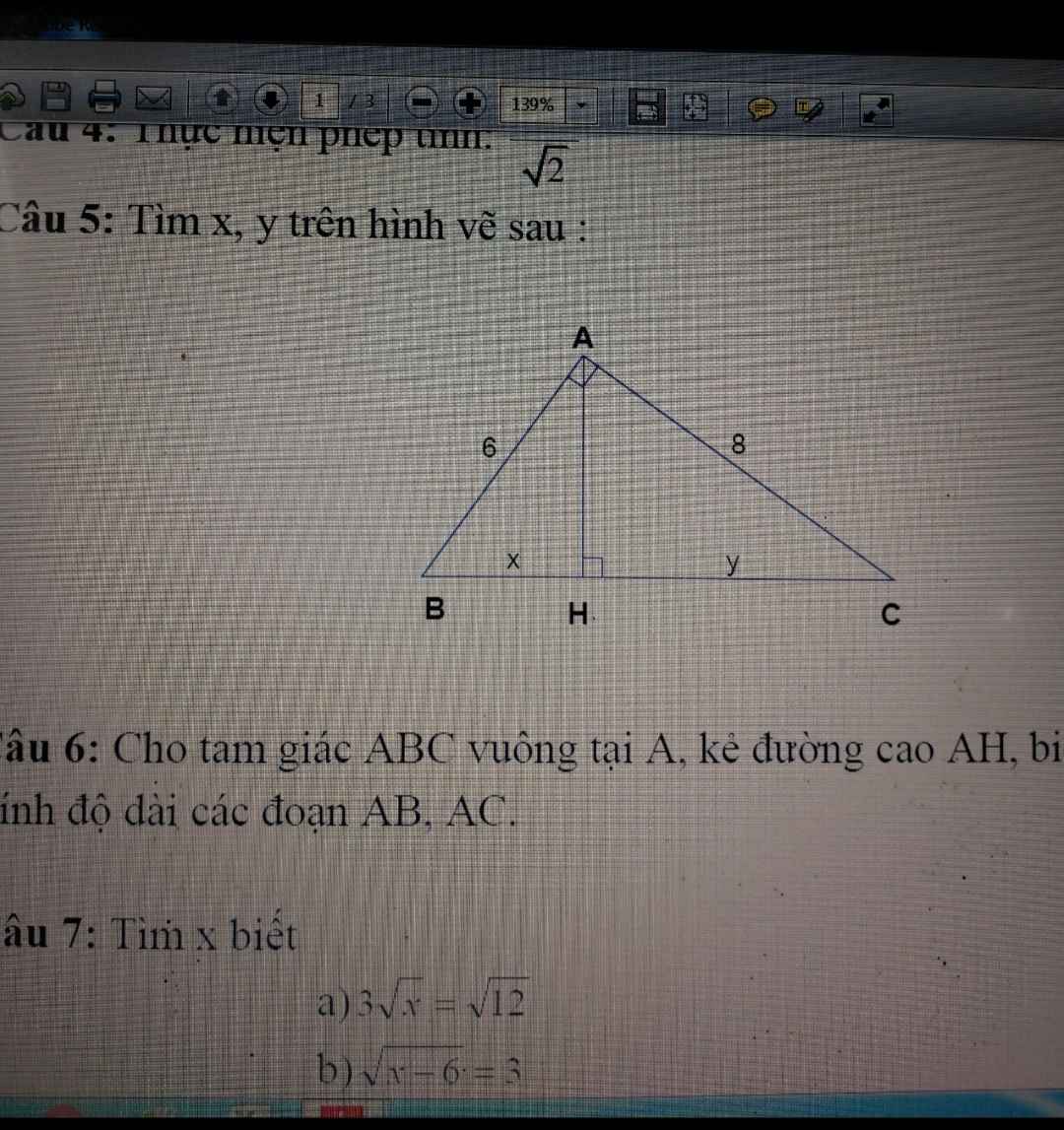
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
NV
19 tháng 7 2019
Bạn chụp ảnh đăng đề bài lên nhà hoặc bạn viết có kí tự ra ko mk ko biết đề bài chính xác là gì
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 12 2021
6.
\(0,3a^3b^2\sqrt{\dfrac{9}{a^4b^8}}=0,3a^3b^2.\dfrac{3}{a^2b^4}=\dfrac{0,9.a}{b^2}\)
Đáp án B
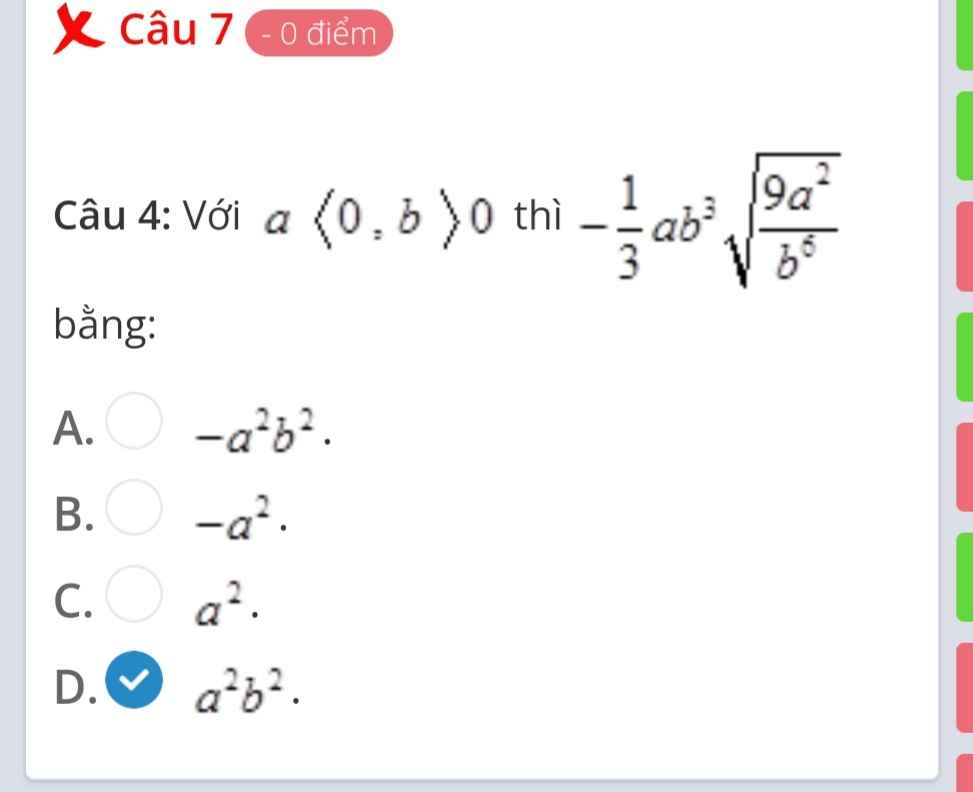
7.
\(-\dfrac{1}{3}ab^3\sqrt{\dfrac{9a^2}{b^6}}=-\dfrac{1}{3}ab^3.\dfrac{3\left|a\right|}{\left|b^3\right|}=-ab^3.\dfrac{-a}{b^3}=a^2\)
Đáp án C
28 tháng 10 2021
\(a,P=\dfrac{3\sqrt{a}-3}{\sqrt{a}\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}-1}\left(a\ge0;a\ne1\right)\\ P=\dfrac{3\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}=\dfrac{3\left(\sqrt{a}+1\right)}{\sqrt{a}}\\ b,a=4\Leftrightarrow\sqrt{a}=2\\ \Leftrightarrow P=\dfrac{3\left(2+1\right)}{2}=\dfrac{9}{2}\)
TN
1
28 tháng 10 2021
\(P=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}}{x-4}.\dfrac{x-4}{-2\sqrt{x}}=\dfrac{2x}{-2\sqrt{x}}=-\sqrt{x}\)
\(P=-\sqrt{x}=-\sqrt{4}=-2\left(đpcm\right)\)
Câu 1:
a) \(A=\dfrac{3}{\sqrt{7}-2}-\dfrac{14}{\sqrt{7}}+\sqrt{\left(\sqrt{7}-2\right)^2}=\dfrac{3\left(\sqrt{7}+2\right)}{7-4}-\dfrac{14\sqrt{7}}{7}+\sqrt{7}-2=\dfrac{3\sqrt{7}+6}{3}-2\sqrt{7}+\sqrt{7}-2=\sqrt{7}+2-2\sqrt{7}+\sqrt{7}-2=0\)
b) \(5x^2-2\sqrt{5}x+1=0\)
\(\Leftrightarrow\left(\sqrt{5}x-1\right)^2=0\)
\(\Leftrightarrow\sqrt{5}x-1=0\Leftrightarrow\sqrt{5}x=1\Leftrightarrow x=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)
c) \(\left\{{}\begin{matrix}3x-2y=16\\x+5y=-23\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=16\\3x+15y=-69\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+5y=-23\\-17y=85\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-5\end{matrix}\right.\)