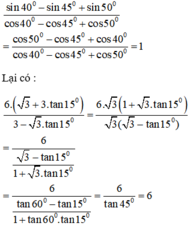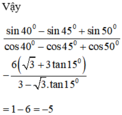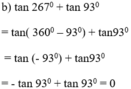Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai bạn được chọn ở HĐ2a có vai trò như nhau, nói cách khác là không quan trọng thứ tự chọn.
Còn ở HĐ2b thì hai bạn có có vai trò khác nhau, nói cách khác là có xếp thứ tự lần lượt là lớp trưởng và lớp phó.
b) Số cách chọn 2 bạn (có xếp thứ tự) là 12 cách chọn.
Nhưng ở HĐ2a thì hai bạn có vai trò như nhau nên ta chia kết quả cho 2, tức là có 6 cách chọn (khi không xếp thứ tự)

Cần đề cụ thể hơn để có thể trả lời chắc chắn, nhưng 99% trong các trường hợp tương tự của bài này thì dùng tổ hợp
Đề đây ạ:
Một hộp đựng 9 thẻ được đánh số 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 . Rút ngẫu nhiên đồng thời hai thẻ và nhân hai số ghi trên hai thẻ lại với nhau. Tính xác suất để kết quả thu được là một số chẵn.
Nhưng em ko hiểu chỗ không gian mẫu, sao lại dùng tổ hợp ạ? Em nghĩ TH bốc thẻ 1 rồi thẻ 2 sẽ tính là 1TH rồi bốc thẻ 2 rồi thẻ 1 sẽ là TH nữa


Ta được

Ta chọn số gần đúng là 1,912931183.
Độ chính xác d=0,0005 nên ta có hàng làm tròn là hàng phần nghìn.
Số ở hàng phần nghìn là số 2, số bên phải là số 9>5 nên ta tăng 2 thêm 1 đơn vị và được số quy tròn của 1,912931183 là 1,913

Bằng máy tính cầm tay, ta tính được kết quả là: \(\sqrt[3]{{15}}:5 - 2 \approx - 1,51\)

Tham khảo:
+) Biểu diễn: \(A \subset B\)
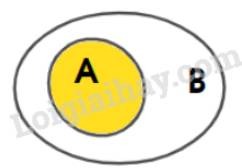
+) Sau đó, biểu diễn: \(B \subset C\)

Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)

Ta có: sin 40º = cos 50º ; sin 45º = cos 45º ; sin 50º = cos 40º
Do đó :