Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
Gọi x(m) là chiều rộng của mảnh đất(Điều kiện: x>0)
Chiều dài của mảnh đất là: x+5(m)
Theo đề, ta có phương trình:
2x+5=25
\(\Leftrightarrow2x=20\)
hay x=10(thỏa ĐK)
Vậy: Diện tích của mảnh đất là 150m2

Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

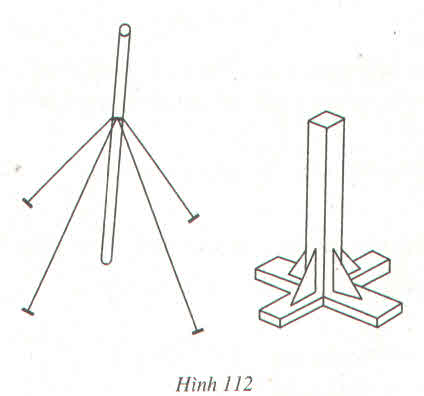
Vì cái cọc hay chân bàn đều vuông góc với mặt phẳng là mặt đất nên để cái cọc hay chân bàn đứng vững người ta dùng ít nhất là 3 điểm không thẳng hàng trên mặt đất để định vị.

- Bạn Hòa giải sai. Vì không thể chia hai vế của phương trình đã cho với x (bởi vì x có thể = 0) để được phương trình x + 2 = x + 3. Làm như thế này có thể làm mất nghiệm của phương trình ban đầu.
- Lời giải đúng:
(Hoặc: x(x + 2) = x(x + 3)
\(\Leftrightarrow\) x(x + 2) - x(x + 3) = 0 (chuyển vế)
\(\Leftrightarrow\) x(x + 2 - x - 3) = 0 (rút nhân tử chung x)
\(\Leftrightarrow\) x.(-1) = 0
\(\Leftrightarrow\) x = 0)

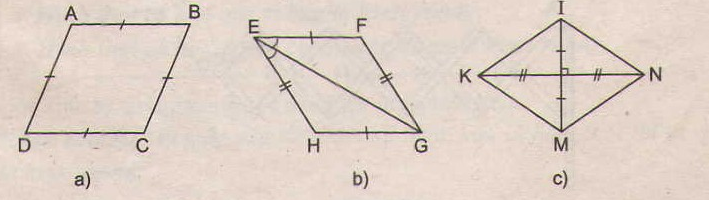
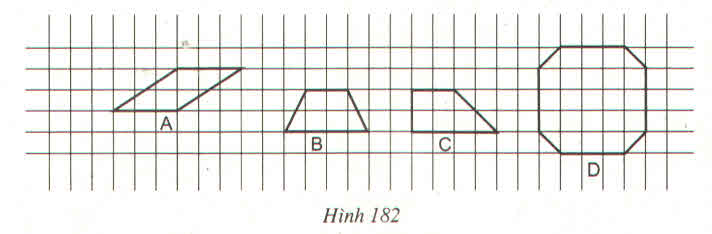
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
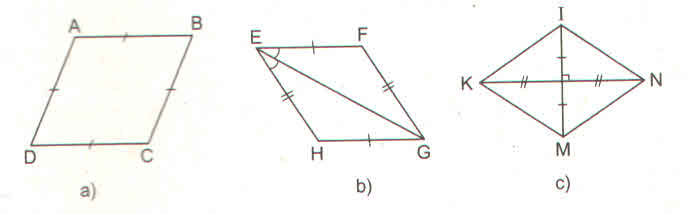
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
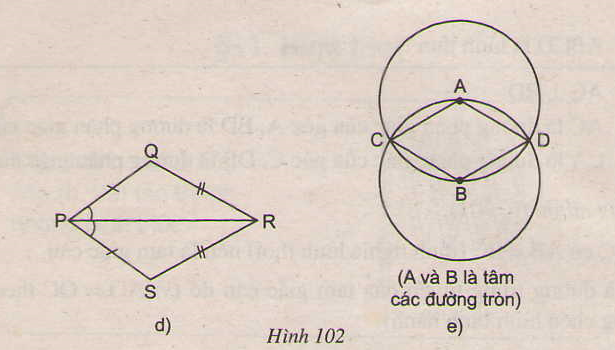
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.

 cd
cd




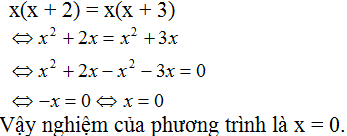


\(\dfrac{2\left(5x+2\right)}{9}-1=\dfrac{4\left(33+2x\right)}{5}-\dfrac{5\left(1-11x\right)}{9}\)
\(\dfrac{10\left(5x+2\right)}{45}-\dfrac{45}{45}=\dfrac{36\left(33+2x\right)}{45}-\dfrac{25\left(1-11x\right)}{45}\)
\(50x-20-45=1188+72x-25+275x\)
\(50x-25=347x+1163\)
\(50x-347x=25+1163\)
\(-297x=1188\)
\(x=4\\ \)
d)
\(\dfrac{2\left(x-4\right)}{3}+\dfrac{3x+13}{8}=\dfrac{2\left(2x-3\right)}{5}+12\)
\(\dfrac{80\left(x-4\right)}{120}+\dfrac{15\left(3x+13\right)}{120}=\dfrac{40\left(2x-3\right)}{120}+\dfrac{1440}{120}\)
\(80x-320+45x+195=80x-120+1440\)
\(125x-125=80x+1320\)
\(125x-80x=125+1320\)
\(45x=1445\)
\(x=\dfrac{1445}{45}\) \(=\dfrac{289}{9}\)
Sai rồi anh ơi 😢
c)S={-4}
d)S={49}
Sách nó viết thế chứ em ko biết nha