Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
Do đó: ADME là hình chữ nhật
b:ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
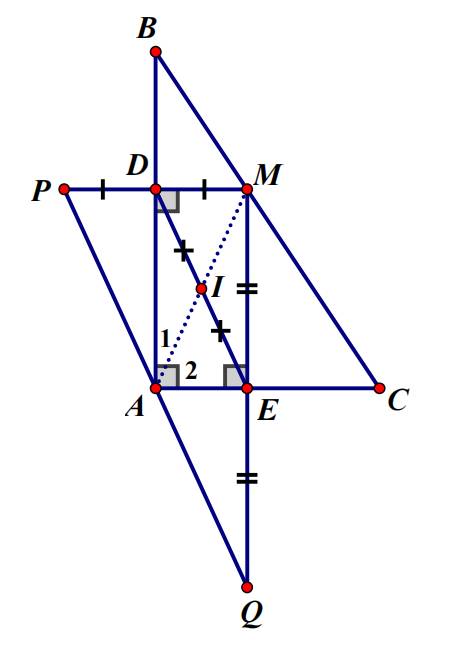
c: Xét ΔAMQ có
AE vừa là đường cao, vừa là trung tuyến
=>ΔAMQ cân tại A
=>AE là phân giác của góc MAQ(1)
Xét ΔAMP có
AD vừa là đường cao, vừa là trung tuyến
=>ΔAMP cân tại A
=>AD là phân giác của góc MAP(2)
Từ (1), (2) suy ra góc PAQ=góc MAP+góc MAQ
=2(góc BAM+góc CAM)
=2*góc BAC
=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ=AM
nên A là trung điểm của PQ

HÌnh bạn tự vẽ nha.
1/Theo định lí đường tb của hình thang thì:
CK=\(\frac{AB+EM}{2}=\frac{10+14}{2}=12\)
2/a/Ta có:TỨ giác AHMK có \(\hept{\begin{cases}gócA=90^o\\gócH=90^o\\gócK=90^o\end{cases}}\)
MÀ AHM+HMK+MKA+KAH=3600 \(\Rightarrow\) HMK=90o
\(\Rightarrow\)Tứ Giác AHMK là HÌnh Chữ Nhật
b/c/d/cm đó dễ mà bạn tự làm đi.

a: Xét tứ giác AMHN có
AM//HN
AN//HM
Do đó: AMHN là hình bình hành
Hình bình hành AMHN có \(\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
b: Ta có: AMHN là hình bình hành
=>HM//AN và HM=AN
Ta có: HM//AN
N\(\in\)AE
Do đó: HM//ND
Ta có: HM=NA
NA=ND
Do đó: HM=ND
Xét tứ giác MHDN có
MH//DN
MH=DN
Do đó: MHDN là hình bình hành
c: Gọi O là giao điểm của AH và NM
Ta có: ANHM là hình chữ nhật
=>AH=MN và AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Ta có: ΔAEH vuông tại E
mà EO là đường trung tuyến
nên \(EO=\dfrac{AH}{2}=\dfrac{MN}{2}\)
Xét ΔNEM có
EO là đường trung tuyến
\(EO=\dfrac{NM}{2}\)
Do đó: ΔNEM vuông tại E
=>NE\(\perp\)ME

a: Xét tứ giác AMHN có
AM//HN
AN//HM
Do đó: AMHN là hình bình hành
Hình bình hành AMHN có \(\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
b: Ta có: AMHN là hình bình hành
=>HM//AN và HM=AN
Ta có: HM//AN
N\(\in\)AE
Do đó: HM//ND
Ta có: HM=NA
NA=ND
Do đó: HM=ND
Xét tứ giác MHDN có
MH//DN
MH=DN
Do đó: MHDN là hình bình hành
c: Gọi O là giao điểm của AH và NM
Ta có: ANHM là hình chữ nhật
=>AH=MN và AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Ta có: ΔAEH vuông tại E
mà EO là đường trung tuyến
nên \(EO=\dfrac{AH}{2}=\dfrac{MN}{2}\)
Xét ΔNEM có
EO là đường trung tuyến
\(EO=\dfrac{NM}{2}\)
Do đó: ΔNEM vuông tại E
=>NE\(\perp\)ME
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+6^2=10^2\)
=>\(AC^2=100-36=64\)
=>\(AC=\sqrt{64}=8\left(cm\right)\)
b: Xét tứ giác ADME có
AD//ME
AE//MD
Do đó: ADME là hình bình hành
Hình bình hành ADME có \(\widehat{DAE}=90^0\)
nên ADME là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{1}{2}BC\)
Ta có: DE//BC
M\(\in\)BC
Do đó: DE//MB
Ta có: \(DE=\dfrac{1}{2}BC\)
\(MC=MB=\dfrac{1}{2}BC\)
Do đó: DE=MC=MB
Xét tứ giác BDEM có
DE//MB
DE=MB
Do đó: BDEM là hình bình hành
d: Xét tứ giác ABCK có
E là trung điểm chung của AC và BK
=>ABCK là hình bình hành
=>AK//BC
Xét tứ giác AMCI có
E là trung điểm chung của AC và MI
=>AMCI là hình bình hành
=>AI//CM
=>AI//BC
Ta có: AI//BC
AK//BC
AI,AK có điểm chung là A
Do đó: A,I,K thẳng hàng