Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔBMP có
BD vừa là đường cao, vừa là đường trung tuyến
Do đó: ΔBMP cân tại B
=>BA là phân giác của góc MBP
Xét ΔAMP có
AD là đường cao, là đường trung tuyến
Do đó: ΔAMP cân tại A
=>AB là phân giác của góc MAP(1)
Xét ΔAMQ có
AC vừa là đường cao, vừa là đường trung tuyến
Do đó; ΔAMQ cân tại A
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*góc BAC=180 độ
=>P,A,Q thẳng hàng
Xét ΔAMB và ΔAPB có
AM=AP
AB chung
BM=BP
Do đó: ΔAMB=ΔAPB
=>góc AMB=góc APB
Xét ΔAMC và ΔAQC có
AM=AQ
góc MAC=góc QAC
AC chung
Do đó: ΔAMC=ΔAQC
=>góc AMC=góc AQC
=>góc AQC+góc AMB=180 độ
mà góc AMB=góc APB
nên góc AQC+góc APB=180 độ
=>BP//QC
=>BPQC là hình thang
d: AM=AP
AM=AQ
Do đó: AP=AQ
mà P,A,Q thẳng hàng
nên A là trung điểm của PQ

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

Hinh nhu de sai thi phai ban ah.Ban thu coi lai coi xem co dieu kien nao cua tam giac ABC khong ?

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
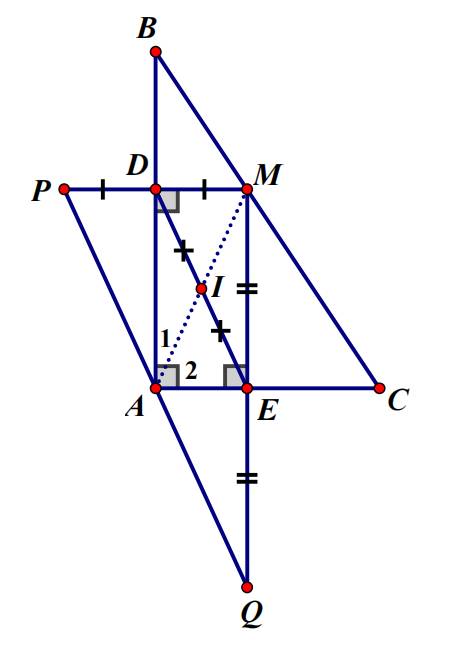
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
Do đó: ADME là hình chữ nhật
b:ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔAMQ có
AE vừa là đường cao, vừa là trung tuyến
=>ΔAMQ cân tại A
=>AE là phân giác của góc MAQ(1)
Xét ΔAMP có
AD vừa là đường cao, vừa là trung tuyến
=>ΔAMP cân tại A
=>AD là phân giác của góc MAP(2)
Từ (1), (2) suy ra góc PAQ=góc MAP+góc MAQ
=2(góc BAM+góc CAM)
=2*góc BAC
=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ=AM
nên A là trung điểm của PQ