
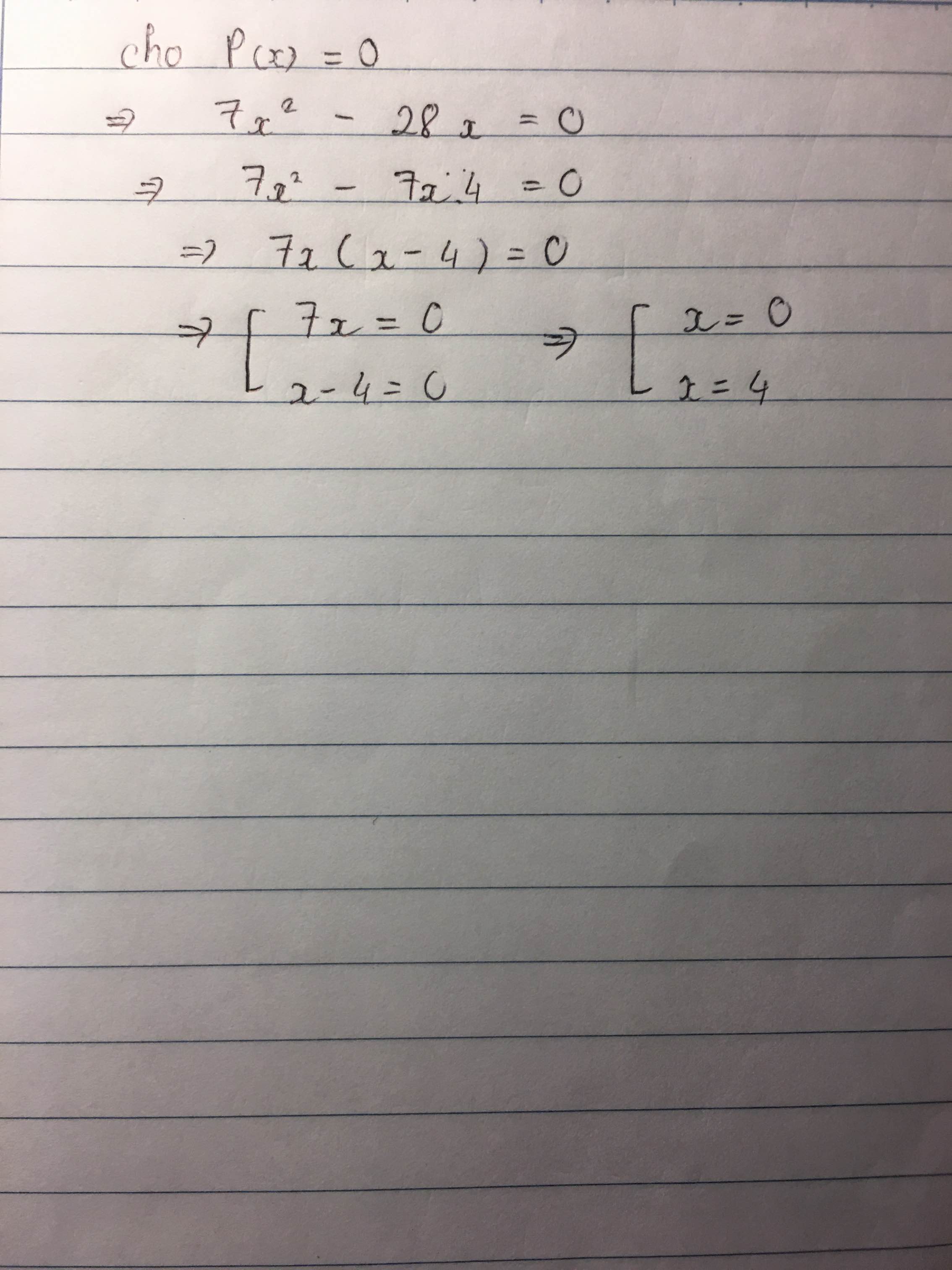
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

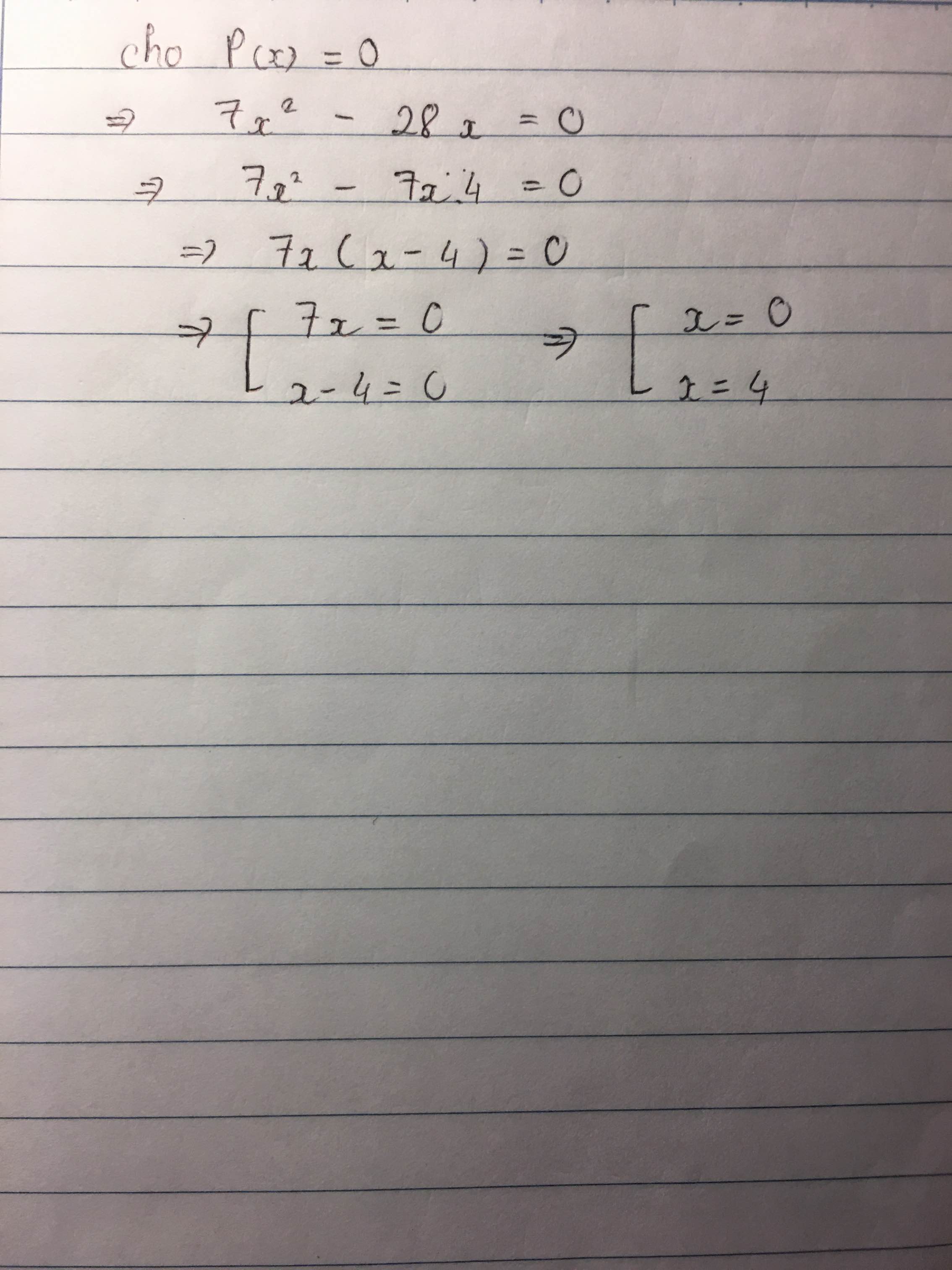

P + Q = (-5x4 +3x3 + 7x2 + x – 3) + (5x4 – 4x3 – x2 + 3x + 3)
= -5x4 +3x3 + 7x2 + x – 3 + 5x4 – 4x3 – x2 + 3x + 3
= (-5x4 + 5x4 ) + (3x3 – 4x3 ) + (7x2 – x2 ) + (x + 3x) + (-3 + 3)
= 0 + (-x3) + 6x2 +4x
= -x3 + 6x2 +4x
P – Q = (-5x4 +3x3 + 7x2 + x – 3) - (5x4 – 4x3 – x2 + 3x + 3)
= -5x4 +3x3 + 7x2 + x – 3 - 5x4 + 4x3 + x2 - 3x - 3
= (-5x4 - 5x4 ) + (3x3 + 4x3 ) + (7x2 + x2 ) + (x - 3x) + (-3 - 3)
= -10x4 + 7x3 + 8x2 + (-2x) + (-6)
= -10x4 + 7x3 + 8x2 – 2x – 6
a) Đa thức P + Q có bậc là 3
Đa thức P – Q có bậc là 4
b) +) Tại x = 1 thì P + Q = - 13 + 6. 12 + 4.1 = 9
P – Q = -10. 14 + 7.13 + 8.12 – 2. 1 – 6 = -3
+) Tại x = - 1 thì P + Q = - (-1)3 + 6. (-1)2 + 4.(-1) = -(-1) + 6.1 - 4 = 3
P – Q = -10. (-1)4 + 7.(-1)3 + 8.(-1)2 – 2. (-1) – 6 = -10 . 1 + 7.(-1) + 8 + 2 – 6 = -13
c) Đa thức P + Q có nghiệm là x = 0 vì đa thức này có hệ số tự do bằng 0.

`#3107.101107`
`A(x) = 3x - 9x^2 + 4x + 5x^3 + 7x^2 + 1`
`= (3x + 4x) - (9x^2 - 7x^2) + 5x^3 + 1`
`= 7x - 2x^2 + 5x^3 + 1`
`B(x) = 5x^3 - 3x^2 + 7x + 10`
`A(x) - B(x) = 7x - 2x^2 + 5x^3 + 1 - (5x^3 - 3x^2 + 7x + 10)`
`= 7x - 2x^2 + 5x^3 + 1 - 5x^3 + 3x^2 - 7x - 10`
`= (7x - 7x) + (3x^2 - 2x^2) + (5x^3 - 5x^3) - (10 - 1)`
`= x^2 - 9`
`=> C(x) = x^2 - 9`
`C(x) = 0`
`=> x^2 - 9 = 0`
`=> x^2 = 9 => x^2 = (+-3)^2 => x = +-3`
Vậy, nghiệm của đa thức `C(x)` là `x \in {3; -3}.`

1:
P(x)=0
=>7x(x-4)=0
=>x=0 hoặc x=4
2:
a: Xét ΔBAD vuông tại B và ΔIAD vuông tại I có
AD chung
góc BAD=góc IAD
=>ΔBAD=ΔIAD
b: Xét ΔDBH vuông tại B và ΔDIC vuông tại I có
DB=DI
góc BDH=góc IDC
=>ΔDBH=ΔDIC
=>DH=DC
c: BD=DI
DI<DC
=>BD<DC
d: AB+BH=AH
AI+IC=AC
mà AB=AI và BH=IC
nên AH=AC
=>ΔAHC cân tại A
mà AK là trung tuyến
nên AK là phân giác của góc HAC
=>A,D,K thẳng hàng

1: P(x)=0
=>7x(x-4)=0
=>x=0 hoặc x=4
2:
a: Xét ΔABD vuông tại B và ΔAID vuông tại I có
AD chung
góc BAD=góc IAD
=>ΔABD=ΔAID
b: Xét ΔDBH vuông tại B và ΔDIC vuông tại I có
DB=DI
góc BDH=góc IDC
=>ΔDBH=ΔDIC
=>DH=DC
c: BD=DI
DI<DC
=>BD<DC
d: AB+BH=AH
AI+IC=AC
mà AB=AI và BH=IC
nên AH=AC
=>ΔAHC cân tại A
mà AK là trung tuyến
nên AK là phân giác của góc HAI
=>A,D,K thẳng hàng

a) Thu gọn:
P(x) = x4+(-7x2+4x2)+(x+6x)-2x3-2
P(x) = x4-3x2+7x-2x3-2
Sắp xếp: P(x) = x4-2x3-3x2+7x-2
Thu gọn:
Q(x) = x4+(-3x+x)+(-5x3+6x3)+1
Q(x) = x4-2x+x3+1
Sắp xếp: Q(x)= x4+ x3-2x+1
b/ Nếu x=2, ta có:
P(2) = 24-2.23-3.22+7.2-2
= 16 - 2.8 - 3.4 + 14 -2
= 16-16-12+14-2
= -12+14-2
= 0
=> x=0 là nghiệm của P(x)
Q(2)= 24+ 23-2.2+1
= 16+8-4+1
= 24-4+1
=21
mà 21≠0
Vậy: x=2 không phải là nghiệm của Q(x)
=>


`a)`
`Q(x)=-2x^{3}+7x^{2}-9x+12`
`b)`
`P(x)+Q(x)=4x^{3}-7x^{2}+3x-12-2x^{3}+7x^{2}-9x+12`
`=2x^{3}-6x`
``
`2P(x)-Q(x)=8x^{3}-14x^{2}+6x-24-2x^{3}+7x^{2}-9x+12`
`=6x^{3}-7x^{2}-3x-12`
`c)`
`P(x)+Q(x)=0`
`->2x^{3}-6x=0`
`->2x(x^{2}-3)=0`
`->x=0` hoặc `x^{2}-3=0`
`->x=0` hoặc `x=+-\sqrt{3}`
a) \(Q=-2x^3+2x^2+12+5x^2-9x=-2x^3+7x^2-9x+12\)
b) \(P+Q=4x^3-7x^2+3x-12-2x^3+7x^2-9x+12=2x^3-6x\)
\(2P-Q=2\left(4x^3-7x^2+3x-12\right)-\left(-2x^3+7x^2-9x+12\right)=8x^3-14x^2+6x-24+2x^3-7x^2+9x-12=10x^3-21x^2+15x-36\)c) \(P+Q=2x^3-6x=0\)
\(\Leftrightarrow2x\left(x^2-3\right)=0\Leftrightarrow\left[{}\begin{matrix}2x=0\\x^2-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\sqrt{3}\end{matrix}\right.\)