Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của phạm văn quyết tâm - Toán lớp 6 - Học toán với OnlineMath
Giả sử d = (a;b). Khi đó ta có:
\(\hept{\begin{cases}a=md\\b=nd\end{cases}};\left(m;n\right)=1\Rightarrow\left[a;b\right]=mnd\)
Ta có: md+2nd=48 và 3mnd+d=114
md+2nd=48⇒d(m+2n)=48
3mnd+d=114⇒d(3mn+1)=114
Suy ra d∈ƯC(48,114)=(6;3;2;1)
Nếu d = 1, ta có: 3mn+1=114⇒3mn=113
Do 113 không chia hết cho 3 nên trường hợp này ko xảy ra.
Nếu d = 2 ta có: 3mn+1=57⇒3mn=56
Do 56 không chia hết cho 3 nên trường hợp này ko xảy ra.
Nếu d = 3 ta có: 3mn+1=38⇒3mn=37
Do 37 không chia hết cho 3 nên trường hợp này ko xảy ra.
Nếu d = 6 ta có: 3mn+1=19⇒3mn=18⇒mn=6
Và m+2n=8
Suy ra m = 2, n = 3 hoặc m = 6, n = 1
Vậy a = 12, b = 36 hoặc a = 36, b = 6.
hok tốt

a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
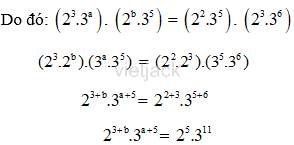
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6

a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

Gọi \(d=ƯCLN\left(a,b\right)\Rightarrow\left\{{}\begin{matrix}a=d.a_1\\b=d.b_1\\UCLN\left(a_1;b_1\right)=1\end{matrix}\right.\)
Mà \(a+2b=48\Rightarrow d.a_1+2d.b_1=48\)
\(d\left(a_1+2b_1\right)=48\) \(\left(1\right)\)
Mà \(ƯCLN\left(a,b\right)+3.BCNN\left(a,b\right)=114\)
\(\Rightarrow d+d.a_1.b_1=114\)
\(d\left(1+3.a_1.b_1\right)\)\(=114\)\(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Rightarrow d\inƯC\left(48;114\right)\)
Mà \(ƯCLN\left(48;114\right)=6\)
\(\Rightarrow d\inƯ\left(6\right)=\left\{1;2;3;6\right\}\)
Rồi bn lần lượt thay \(d\) vào \(\left(1\right)\) và \(\left(2\right)\) bn sẽ thấy được chỉ có \(d=6\) là thỏa mãn
\(+\))\(d=6\) ta có bảng sau :
| \(a_1\) | \(b_1\) | \(a\) | \(b\) | \(Đk\) \(a,b\in N\) |
| \(2\) | \(3\) | \(12\) | \(18\) | \(TM\) |
| \(6\) | \(1\) | \(36\) | \(6\) | \(TM\) |
Vậy cặp giá trị \(\left(a,b\right)\) cần tìm là :
\(\left(12;36\right);\left(18;6\right)\)

Lời giải:
Vì $ƯCLN(a,b)=21$ nên đặt $a=21x, b=21y$ với $x,y$ là stn, $x,y$ nguyên tố cùng nhau.
Ta có:
$BCNN(a,b)=21xy=420\Rightarrow xy=20$ (1)
$a+21=b$
$\Rightarrow 21x+21=21y$
$\Rightarrow x+1=y$ (2)
Từ $(1); (2)$ và $x,y$ là 2 số nguyên tố cùng nhau nên $x=4, y=5$
$\Rightarrow a=21x=21.4=84; b=21y=21.5=105$

Em tham khảo tại link dưới đây nhé.
Câu hỏi của phạm văn quyết tâm - Toán lớp 6 - Học toán với OnlineMath
Giả sử d = (a;b). Khi đó ta có:
\(\hept{\begin{cases}a=md\\b=nd\end{cases}};\left(m;n\right)=1\Rightarrow\left[a;b\right]=mnd\)
Ta có: md+2nd=48 và 3mnd+d=114
md+2nd=48⇒d(m+2n)=48
3mnd+d=114⇒d(3mn+1)=114
Suy ra d∈ƯC(48,114)=(6;3;2;1)
Nếu d = 1, ta có: 3mn+1=114⇒3mn=113
Do 113 không chia hết cho 3 nên trường hợp này ko xảy ra.
Nếu d = 2 ta có: 3mn+1=57⇒3mn=56
Do 56 không chia hết cho 3 nên trường hợp này ko xảy ra.
Nếu d = 3 ta có: 3mn+1=38⇒3mn=37
Do 37 không chia hết cho 3 nên trường hợp này ko xảy ra.
Nếu d = 6 ta có: 3mn+1=19⇒3mn=18⇒mn=6
Và m+2n=8
Suy ra m = 2, n = 3 hoặc m = 6, n = 1
Vậy a = 12, b = 36 hoặc a = 36, b = 6.
hok tốt

Ta có: UCLN(a;b) = 15 => a = 15m và b = 15n (Với m ; n khác 0)
Ta lại có: BCNN(a;b) = 300
Mà: a . b = BCNN(a;b) . UCLN(a;b)
=> a . b = 300 . 15 = 4500 (*)
Ta thay a = 15m và b = 15n vào (*) ta được: 15m . 15n = 4500
=> 225 . mn = 4500 => mn = 4500 : 225 => mn = 20
Do: m và n là sso tự nhiên nên mn = 4 . 5 = 1 . 20
+) Với m = 4 và n = 5 thì a = 60 và b = 75
+) Với m = 5 và n = 4 thì a = 75 và b = 60
+) Với m = 1 và n = 20 thì a = 15 và b = 300
+) Với m = 20 và n = 1 thì a = 300 và b = 15
Ta có : ƯCLN ( a , b ) = 15 => a = 15m và b = 15n ( m ; n \(\ne\) 0 ).
Ta lại có : BCNN ( a ; b ) = 300
Mà a . b = BCNN ( a ; b ) . ƯCLN ( a ; b )
=> a . b = 300 . 15 = 4500 (*)
Thay a = 15m và b = 15n vào (*) ta được :
15m . 15n = 4500
<=> ( 15 . 15 ) mn = 4500
<=> 225mn = 4500
<=> mn = 4500 : 225
<=> mn = 20
Do m và n là số tự nhiên nên mn = 4 . 5 = 1 . 20
=> Ta có bảng :
| m | 4 | 5 | 1 | 20 |
| n | 5 | 4 | 20 | 1 |
| a | 60 | 75 | 15 | 300 |
| b | 75 | 60 | 300 | 15 |