Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

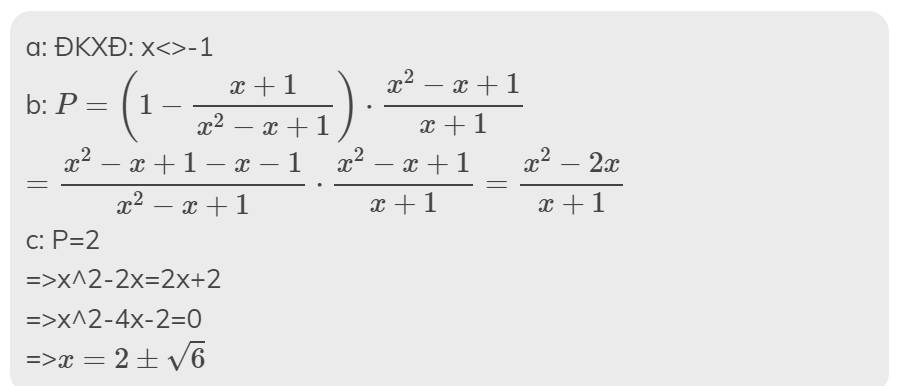
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)

a: ĐKXĐ: x<>4; x<>-4
b: \(A=\dfrac{\left(x-4\right)\left(x-1\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{x-1}{x+4}\)
c: Để A nguyên thì x+4-5 chia hết cho x+4
=>\(x+4\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{-3;-5;1;-9\right\}\)

a: ĐKXĐ: \(x\notin\left\{-\dfrac{1}{2};\dfrac{1}{2};-2\right\}\)
b: \(B=\dfrac{4x^2+4x+1-4-4x^2+4x-1}{\left(2x-1\right)\left(2x+1\right)}\cdot\dfrac{2x+1}{x+2}\)
\(=\dfrac{8x-4}{2x-1}\cdot\dfrac{1}{x+2}=\dfrac{4}{x+2}\)

a) ĐK: \(x\ne4,x\ne2;x\ne-2\)
b) \(A=\dfrac{x^3}{x-4}-\dfrac{x}{x-2}-\dfrac{2}{x+2}\)
\(A=\dfrac{x^3}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(A=\dfrac{x^3-x^2-2x-2x+4}{\left(x+2\right)\left(x-2\right)}\)
\(A=\dfrac{x^3-x^2-4x+4}{\left(x+2\right)\left(x-2\right)}\)
\(A=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x+2\right)\left(x-2\right)}\)
\(A=\dfrac{\left(x-1\right)\left(x^2-4\right)}{x^2-4}\)
\(A=x-1\)
c) \(A=0\) khi:
\(x-1=0\)
\(\Leftrightarrow x=1\left(tm\right)\)
d) A dương khi: \(A>0\)
\(x-1>0\)
\(\Leftrightarrow x>1\)
Kết hợp với đk:
\(x>1,x\ne4,x\ne2\)

a: \(A=\left(\dfrac{x}{x^2-4}+\dfrac{4}{x-2}+\dfrac{1}{x+2}\right):\dfrac{3x+3}{x^2+2x}\)
\(=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x\left(x+2\right)}{3\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{x-2}\)

1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)

Lời giải:
a.
ĐKXĐ: $x\neq \pm 2$
b.
\(P=\left[\frac{4(x-2)}{(x+2)(x-2)}+\frac{3(x+2)}{(x+2)(x-2)}-\frac{5x+2}{(x-2)(x+2)}\right].\frac{x+2}{2}\)
\(=\frac{4(x-2)+3(x+2)-(5x+2)}{(x-2)(x+2)}.\frac{x+2}{2}=\frac{2(x-2)}{(x-2)(x+2)}.\frac{x+2}{2}=1\)

giú mới ạ mái em noppj rồi