Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \({u_3} = {u_1}.{q^2} \Leftrightarrow \left( {\frac{{27}}{4}} \right) = 3.{q^2} \Leftrightarrow q = \frac{3}{2}\)
Năm số hạng đầu của cấp số nhân: \(3;\frac{9}{2};\frac{{27}}{4};\frac{{81}}{8};\frac{{243}}{{16}}\)
b) Tổng 10 số hạng đầu:
\({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}} = \frac{{3\left( {1 - {{\left( {\frac{3}{2}} \right)}^{10}}} \right)}}{{1 - \frac{3}{2}}} = \frac{{3.\frac{{ - 58025}}{{1024}}}}{{1 - \frac{3}{2}}} = \frac{{ - 174075}}{{1024}}.\left( { - 2} \right) = \frac{{174075}}{{512}}\)

a) \({u_1} = 5,\;\;{u_2} = 10,\;\;\;{u_3} = 15,\;\;{u_4} = 20,\;\;\;{u_5} = 25\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{5n}}{{5n - 1}} \)phụ thuộc vào n.
Suy ra dãy số \(\left( {{u_n}} \right)\) không phải là cấp số nhân.
b) \({u_1} = 5,\;\;{u_2} = 25,\;\;{u_3} = 125,\;\;\;{u_4} = 625,\;\;\;{u_5} = 3125\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{{5^n}}}{{{5^{n - 1}}}} = 5,\;\forall n \ge 2\).
Do đó dãy số \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 5\).
Số hạng tổng quát: \({u_n} = 5 \times {5^{n - 1}}= 5^{n}\).
c) \({u_1} = 1,\;\;\;{u_2} = 2,\;\;\;{u_3} = 6,\;\;\;{u_4} = 24,\;\;\;{u_5} = 120\).
có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = n\) phụ thuộc vào n, \(\forall n \in {N^*}\).
Suy ra dãy số \(\left( {{u_n}} \right)\) không phải là cấp số nhân.
d) \({u_1} = 1,\;\;{u_2} = 5,\;\;{u_3} = 25,\;\;\;{u_4} = 125,\;\;\;{u_5} = 625\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = 5,\;\forall n \ge 2\).
Do đó dãy số \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 5\).
Số hạng tổng quát: \({u_n} = {5^{n - 1}}\).

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
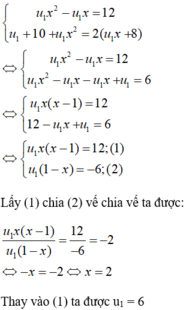
+ Tổng của năm số hạng đầu của CSN là:


a) Ta có:
- Số hạng thứ nhất: \({u_1}\)
- Số hạng thứ hai: \({u_2} = {u_1}.q\)
- Số hạng thứ ba: \({u_3} = {u_2}.q = \left( {{u_1}.q} \right).q = {u_1}.{q^2}\)
- Số hạng thứ tư: \({u_4} = {u_3}.q = \left( {{u_1}.{q^2}} \right).q = {u_1}.{q^3}\)
- Số hạng thứ năm: \({u_5} = {u_4}.q = \left( {{u_1}.{q^3}} \right).q = {u_1}.{q^4}\)
b) Dự đoán công thức tính: \({u_n} = {u_1}.{q^{n - 1}}\)

Ta có: \({S_n} = \frac{{5\left( {1 - {2^n}} \right)}}{{1 - 2}} = - 5 + 5 \times {2^n}\;\)
\(\begin{array}{l}5115 = - 5 + {5.2^n}\\ \Leftrightarrow {2^n} = 1024 = 2.\\ \Rightarrow n = 10.\end{array}\)
Vậy phải lấy tổng 10 số hạng đầu.

a) \({u_9} = {u_1}.{q^{9 - 1}} = \left( { - 5} \right){.2^8} = - 1280\)
b) Ta có: \( - 320 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = 64 \Leftrightarrow n = 7\)
\( - 320\) là số hạng thứ 7 của cấp số nhân
c) Ta có: \(160 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = - {2^5}\)
160 không là số hạng của cấp số nhân

Gọi 4 số cần tìm là \(a_1,a_2,a_3,a_4\). Theo đầu bài ta có hệ :
\(\begin{cases}a_2^2=a_1a_3\\2a_3=a_2+a_4\\a_1+a_4=14\\a_2+a_3=12\end{cases}\) \(\Leftrightarrow\begin{cases}2a_1q^2=a_1q+a_2+d\left(1\right)\\a_1+a_2+d=14\left(2\right)\\a_1q+a_1q^2=12\left(3\right)\\a_2+a_2+d=12\left(4\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2^2=a_1\left(a_2+d\right)\left(5\right)\\a_2+2d=14-a_1\\a_1=\frac{12}{q+q^2}\\d=12-2a_2\end{cases}\)
Giải hệ thống các phương trình ta có kết quả \(\left(2,4,8,12\right)\left(\frac{25}{2},\frac{15}{2}\frac{9}{2}\frac{3}{2}\right)\)

a) Cấp số nhân có số hạng đầu \({u_1} = 5\) và công bội \(q = 2\).
Vậy ta có: \({u_n} = {u_1}.{q^{n - 1}} = {5.2^{n - 1}}\)
b) Cấp số nhân có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{{10}}\).
Vậy ta có: \({u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{10}}} \right)^{n - 1}} = \frac{1}{{{{10}^{n - 1}}}}\).

Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
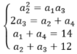
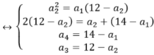
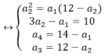
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D
Tổng số lương của chuyên gia đó sau 10 năm là:
\(S=\dfrac{10\cdot\left[2\cdot240+10\cdot1.05\right]}{2}=2452.5\left(đồng\right)\)