Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: (5x-1)(x-3)<0
nên 5x-1 và x-3 trái dấu
Trường hợp 1:
\(\left\{{}\begin{matrix}5x-1>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{5}\\x< 3\end{matrix}\right.\Leftrightarrow\dfrac{1}{5}< x< 3\)
Trường hợp 2:
\(\left\{{}\begin{matrix}5x-1< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{1}{5}\\x>3\end{matrix}\right.\Leftrightarrow loại\)
Vậy: S={x|\(\dfrac{1}{5}< x< 3\)}

*vn:vô nghiệm.
a. \(\left(x^2-2\right)\left(x^2+x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2=0\\x^2+x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
-Vậy \(S=\left\{\pm\sqrt{2}\right\}\).
b. \(16x^2-8x+5=0\)
\(\Leftrightarrow16x^2-8x+1+4=0\)
\(\Leftrightarrow\left(4x-1\right)^2+4=0\) (vô lí)
-Vậy S=∅.
c. \(2x^3-x^2-8x+4=0\)
\(\Leftrightarrow x^2\left(2x-1\right)-4\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\pm2\end{matrix}\right.\)
-Vậy \(S=\left\{\dfrac{1}{2};\pm2\right\}\).
d. \(3x^3+6x^2-75x-150=0\)
\(\Leftrightarrow3x^2\left(x+2\right)-75\left(x+2\right)=0\)
\(\Leftrightarrow3\left(x+2\right)\left(x^2-25\right)=0\)
\(\Leftrightarrow3\left(x+2\right)\left(x+5\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\pm5\end{matrix}\right.\)
-Vậy \(S=\left\{-2;\pm5\right\}\)

Bài 1:
a.
$(4x^2+4x+1)-x^2=0$
$\Leftrightarrow (2x+1)^2-x^2=0$
$\Leftrightarrow (2x+1-x)(2x+1+x)=0$
$\Leftrightarrow (x+1)(3x+1)=0$
$\Rightarrow x+1=0$ hoặc $3x+1=0$
$\Rightarrow x=-1$ hoặc $x=-\frac{1}{3}$
b.
$x^2-2x+1=4$
$\Leftrightarrow (x-1)^2=2^2$
$\Leftrightarrow (x-1)^2-2^2=0$
$\Leftrightarrow (x-1-2)(x-1+2)=0$
$\Leftrightarrow (x-3)(x+1)=0$
$\Leftrightarrow x-3=0$ hoặc $x+1=0$
$\Leftrightarrow x=3$ hoặc $x=-1$
c.
$x^2-5x+6=0$
$\Leftrightarrow (x^2-2x)-(3x-6)=0$
$\Leftrightarrow x(x-2)-3(x-2)=0$
$\Leftrightarrow (x-2)(x-3)=0$
$\Leftrightarrow x-2=0$ hoặc $x-3=0$
$\Leftrightarrow x=2$ hoặc $x=3$
2c.
ĐKXĐ: $x\neq 0$
PT $\Leftrightarrow x-\frac{6}{x}=x+\frac{3}{2}$
$\Leftrightarrow -\frac{6}{x}=\frac{3}{2}$
$\Leftrightarrow x=-4$ (tm)
2d.
ĐKXĐ: $x\neq 2$
PT $\Leftrightarrow \frac{1+3(x-2)}{x-2}=\frac{3-x}{x-2}$
$\Leftrightarrow \frac{3x-5}{x-2}=\frac{3-x}{x-2}$
$\Rightarrow 3x-5=3-x$
$\Leftrightarrow 4x=8$
$\Leftrightarrow x=2$ (không tm)
Vậy pt vô nghiệm.

Bài 2 :
a, \(\frac{1-5x}{x-1}\ge1\)
\(\Leftrightarrow\frac{1-5x}{x-1}\ge\frac{x-1}{x-1}\)
\(\Rightarrow1-5x\ge x-1\)
\(\Leftrightarrow-5x-x\ge-1-1\)
\(\Leftrightarrow-6x\ge-2\)
\(\Leftrightarrow x\le\frac{1}{3}\)
Vậy nghiệm của bất phương trình là \(x\le\frac{1}{3}\).
b, \(\frac{x}{x-2}-\frac{2}{x-3}>1\)
\(\Leftrightarrow\frac{x^2-3x}{x^2-5x+6}-\frac{2x-4}{x^2-5x+6}>\frac{x^2-5x+6}{x^2-5x+6}\)
\(\Rightarrow x^2-3x-2x+4>x^2-5x+6\)
\(\Leftrightarrow x^2-3x-2x-x^2+5x>6-4\)
\(\Leftrightarrow0>2\) ( vô lí )
Vậy bất phương trình vô nghiệm.
Bài 1:
a, \(x^2-8x< 0\)
\(\Leftrightarrow x\left(x-8\right)< 0\)
\(\Leftrightarrow x< 0\) hoặc \(x-8< 0\)
\(\Leftrightarrow x< 0\) hoặc \(x< 8\)
Vậy nghiệm của bất phương trình : x<0 ; x<8
b, \(x^2< 6x-5\)
\(\Leftrightarrow x^2-6x+5< 0\)
\(\Leftrightarrow x^2-x-5x+5< 0\)
\(\Leftrightarrow x\left(x-1\right)-5\left(x-1\right)< 0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\) \(x-1< \) 0 hoặc \(x-5< 0\)
\(\Leftrightarrow x< 1\) hoặc \(x< 5\)
Vậy bất phương trình có nghiệm là x<1 ; x<5

\(a,x^3+x^2+x+1=0\\ \Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\\ \Rightarrow\left(x^2+1\right)\left(x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-1\right\}\)
\(b,x^3+x^2-x-1=0\\ \Rightarrow x^2\left(x+1\right)-\left(x+1\right)=0\\ \Rightarrow\left(x^2-1\right)\left(x+1\right)=0\\ \Rightarrow\left(x-1\right)\left(x+1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-1;1\right\}\)
\(c,\left(x+1\right)^2\left(x+2\right)+\left(x+1\right)^2\left(x-2\right)=-24\\ \Rightarrow\left(x+1\right)^2\left(x+2+x-2\right)=-24\\ \Rightarrow2x\left(x^2+2x+1\right)=-24\\ \Rightarrow x^3+2x^2+x+12=0\\ \Rightarrow\left(x^3+3x^2\right)-\left(x^2+3x\right)+\left(4x+12\right)=0\\ \Rightarrow x^2\left(x+3\right)-x\left(x+3\right)+4\left(x+3\right)=0\\ \Rightarrow\left(x^2-x+4\right)\left(x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-\dfrac{1}{2}\right)^2+\dfrac{15}{4}=0\left(vô.lí\right)\\x=-3\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-3\right\}\)

a: \(\Leftrightarrow x^2-4-4x^2-4x-1-2x+3x^2=0\)
=>-6x-5=0
=>-6x=5
hay x=-5/6
b: \(\Leftrightarrow2x^3+8x^2+8x-8x^2-2x^3+16=0\)
=>8x+16=0
hay x=-2
c: \(\Leftrightarrow x^3-6x^2+12x-8+9x^2-1-x^3-3x^2-3x-1=0\)
=>9x-10=0
hay x=10/9
d: \(\Leftrightarrow10x-15-20x+28=19-2x^2-4x-2\)
\(\Leftrightarrow-10x+13+2x^2+4x-17=0\)
\(\Leftrightarrow2x^2-6x-4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{17}}{2}\\x_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)
Bài 1: Giải các bất phương trình sau
a) x+1/x+3 > 1
b) 2x-1/x-3 ≤ 2
c) x2+2x+2/x2+3 ≥ 1
d) 2x+1/x2+2 ≥ 1

a, \(\dfrac{x+1}{x+3}>1\Leftrightarrow\dfrac{x+1}{x+3}-1>0\Leftrightarrow\dfrac{x+1-x-3}{x+3}>0\)
\(\Rightarrow x+3< 0\)do -2 < 0
\(\Rightarrow x< -3\)Vậy tập nghiệm BFT là S = { x | x < -3 }
b, \(\dfrac{2x-1}{x-3}\le2\Leftrightarrow\dfrac{2x-1}{x-3}-2\le0\Leftrightarrow\dfrac{2x-1-2x+6}{x-3}\le0\)
\(\Rightarrow x-3\le0\)do 5 > 0
\(\Rightarrow x\le3\)Vậy tập nghiệm BFT là S = { x | x \(\le\)3 }
c, \(\dfrac{x^2+2x+2}{x^2+3}\ge1\Leftrightarrow\dfrac{x^2+2x+2}{x^2+3}-1\ge0\)
\(\Leftrightarrow\dfrac{x^2+2x+2-x^2-3}{x^2+3}\ge0\Rightarrow2x-1\ge0\)do x^2 + 3 > 0
\(\Rightarrow x\ge\dfrac{1}{2}\)Vậy tập nghiệm BFT là S = { x | x \(\ge\)1/2 }
mình ko chắc nên mình đăng sau :>
d, \(\dfrac{2x+1}{x^2+2}\ge1\Leftrightarrow\dfrac{2x+1}{x^2+2}-1\ge0\Leftrightarrow\dfrac{2x+1-x^2-2}{x^2+2}\ge0\)
\(\Rightarrow-x^2+2x-1\ge0\Rightarrow-\left(x-1\right)^2\ge0\)vô lí

\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)
d: \(\Leftrightarrow3x^2-6x-2x+4=0\)
=>(x-2)(3x-2)=0
=>x=2 hoặc x=2/3
e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)
=>x(x-3)(x+1)=0
hay \(x\in\left\{0;3;-1\right\}\)
f: \(\Leftrightarrow x^2-5x-2+x=0\)
\(\Leftrightarrow x^2-4x-2=0\)
\(\Leftrightarrow\left(x-2\right)^2=6\)
hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)
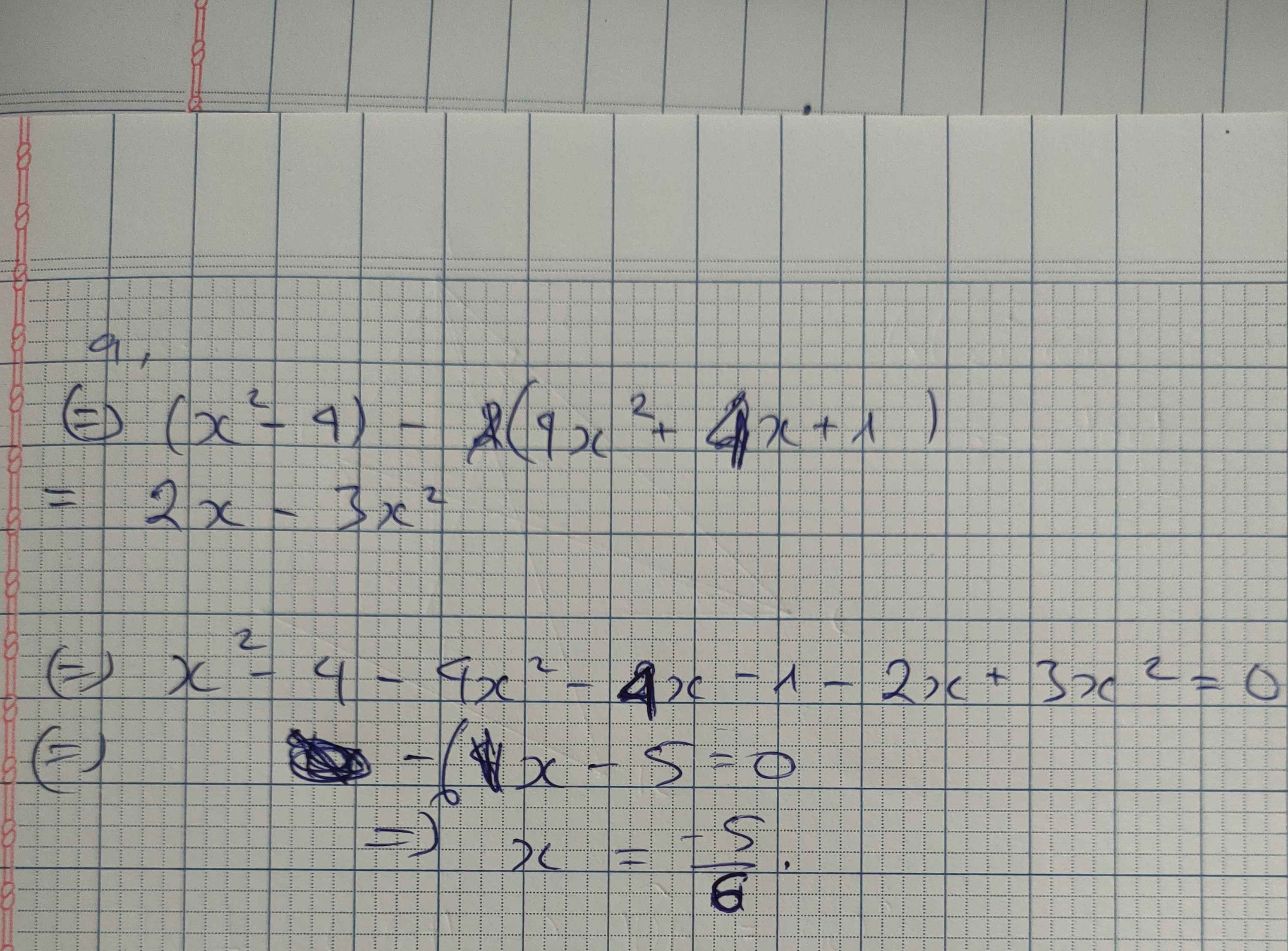
1a
x^2-8x<0
<=> x(x-8)<0
th1: x<0 và x-8>0
x<0 và x>8
<=> 8<x<0 ( vô lý)
th2: x>0 và x-8<0
<=> x>0 và x<8
<=> 0<x<8( tm)
vậy........
a) \(x^2-8x< 0\)
\(\Leftrightarrow x\left(x-8\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}x>0\\x-8< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x< 0\\x-8>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>0\\x< 8\end{cases}}\) hoặc \(\hept{\begin{cases}x< 0\\x>8\end{cases}}\) (loại)
\(\Leftrightarrow0< x< 8\)
b) \(x^2< 6x-5\)
\(\Leftrightarrow x^2-6x+5< 0\)
\(\Leftrightarrow x^2-x-5x+5< 0\)
\(\Leftrightarrow x\left(x-1\right)-5\left(x-1\right)< 0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-1>0\\x-5< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x-1< 0\\x-5>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1\\x< 5\end{cases}}\) hoặc \(\hept{\begin{cases}x< 1\\x>5\end{cases}}\) (loại)
\(\Leftrightarrow1< x< 5\)
c) \(\frac{x-3}{x-2}< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-3>0\\x-2< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x-3< 0\\x-2>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>3\\x< 2\end{cases}}\) (loại) hoặc \(\hept{\begin{cases}x< 3\\x>2\end{cases}}\)
\(\Leftrightarrow2< x< 3\)
d) \(\frac{x+1}{x-3}>2\) (ĐK: \(x\ne3\) )
\(\Leftrightarrow\frac{x+1}{x-3}-2>0\)
\(\Leftrightarrow\frac{x+1-2\left(x-3\right)}{x-3}>0\)
\(\Leftrightarrow\frac{-x+7}{x-3}>0\)
\(\Leftrightarrow\hept{\begin{cases}-x+7>0\\x-3>0\end{cases}}\) hoặc \(\hept{\begin{cases}-x+7< 0\\x-3< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-x>-7\\x>3\end{cases}}\) hoặc \(\hept{\begin{cases}-x< -7\\x< 3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x< 7\\x>3\end{cases}}\) hoặc \(\hept{\begin{cases}x>7\\x< 3\end{cases}}\) (loại)
\(\Leftrightarrow3< x< 7\)