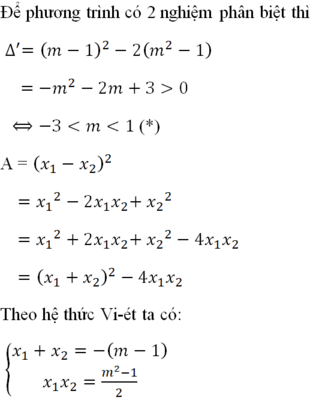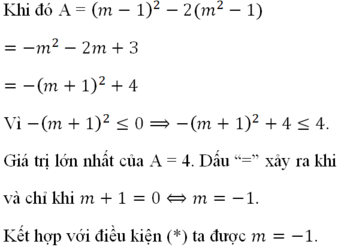Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|\overrightarrow{a}+\overrightarrow{a}\right|=\left|2\overrightarrow{a}\right|=2\left|\overrightarrow{a}\right|=2.50=100\)

\(\hept{\begin{cases}mx+y=m^2+m+1\\-x+my=m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(my-m^2\right)+y-m^2-m-1=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}\left(m^2y-m^2\right)+\left(y-1\right)-\left(m^3+m\right)=0\\x=my-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m^2+1\right)\left(y-m-1\right)=0\\x=my-m^2\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}y=m+1\\x=m\left(m+1\right)-m^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=m\\y=m+1\end{cases}}\)
\(\Rightarrow\)\(x^2+y^2=2m^2+2m+1=2\left(m+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\)
Dấu "=" xảy ra khi \(m=\frac{-1}{2}\) hay hệ có nghiệm \(\left(x;y\right)=\left(\frac{-1}{2};\frac{1}{2}\right)\)

Ta có: D = 2 − 1 1 2 = 5 ≠ 0
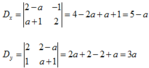
Vì D ≠ 0 nên hệ phương trình có nghiệm duy nhất
x = D x D = 5 − a 5 ; y = D y D = 3 a 5
Khi đó:
x 2 + y 2 = 5 − a 5 2 + 3 a 5 2
= 25 − 10 a + 10 a 2 25 = 10 25 a 2 − a + 1 = 2 5 a − 1 2 2 + 9 10 ≥ 9 10
Dấu “=” xảy ra ⇔ a = 1 2
Đáp án cần chọn là: C

\(\Delta=\left(m+1\right)^2-4\left(m^2-2m+2\right)=-3m^2+10m-7\ge0\)
\(\Rightarrow1\le m\le\dfrac{7}{3}\)
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m^2-2m+2\end{matrix}\right.\)
\(P=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+1\right)^2-2\left(m^2-2m+2\right)\)
\(=-m^2+6m-3\)
\(=\left(-m^2+6m-\dfrac{77}{9}\right)+\dfrac{50}{9}\)
\(=\left(\dfrac{11}{3}-m\right)\left(m-\dfrac{7}{3}\right)+\dfrac{50}{9}\le\dfrac{50}{9}\)
\(P_{max}=\dfrac{50}{9}\) khi \(m=\dfrac{7}{3}\)

Hình như đề thiếu, pt: \(x^2-\left(m+1\right)x+m-2=0\)
Phương trình đã cho có nghiệm khi \(\Delta=\left(m+1\right)^2-4\left(m-2\right)=m^2-2m+9>0\)
\(\Rightarrow\) Phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị m
Định lí Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m-2\end{matrix}\right.\)
a, Theo giả thiết ta có: \(x_1^2+x_2^2=100\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=100\)
\(\Leftrightarrow\left(m+1\right)^2-2\left(m-2\right)=100\)
\(\Leftrightarrow m^2+2m+1-2m+4=100\)
\(\Leftrightarrow m^2=95\)
\(\Leftrightarrow m=\sqrt{95}\)
b, \(P=\left|x_1-x_2\right|\)
\(P^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(m+1\right)^2-4\left(m-2\right)\)
\(=m^2-2m+9=\left(m-1\right)^2+8\ge8\)
\(\Rightarrow P=\left|x_1-x_2\right|\ge2\sqrt{2}\)
\(minP=2\sqrt{2}\Leftrightarrow m=1\)

Phương trình có hai nghiệm
![]()
B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2
= 2 ( x 1 + x 2 ) 2 − 4 x 1 x 2 + 16 − 3 x 1 x 2 = 2 ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) + 16 − 3 ( m 2 + 2 ) = 4 m 2 + 16 m + 16 − 3 ( m 2 + 2 ) = 2 m + 4 − 3 ( m 2 + 2 ) = − 3 m 2 + 2 m − 2
Xét hàm số y = − 3 m 2 + 2 m − 2 với m ≥ 1 2
Bảng biến thiên
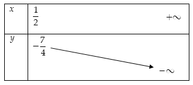
Suy ra giá trị m a x m ≥ 1 2 y = − 7 4 khi m = 1 2
Vậy giá trị lớn nhất của biểu thức B là - 7 4 khi m = 1 2
Đáp án cần chọn là: B

\(\Delta=\left(3m+2\right)^2-12m=9m^2+4>0\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3m-2\\x_1x_2=3m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+1+x_2+1=-3m\\x_1x_2+x_1+x_2+1=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+1+x_2+1=-3m\\\left(x_1+1\right)\left(x_2+1\right)=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x_1+1=a\\x_2+1=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+b=-3m\\ab=-1\end{matrix}\right.\)
\(Q=a^4+b^4\ge2a^2b^2=2\)
Dấu "=" xảy ra khi \(a^2=b^2\Rightarrow\left[{}\begin{matrix}a=b\left(loại\right)\\a=-b\end{matrix}\right.\)
\(\Rightarrow-3m=0\Rightarrow m=0\)