
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



8:
\(=\dfrac{cos10-\sqrt{3}\cdot sin10}{sin10\cdot cos10}=\dfrac{2\left(\dfrac{1}{2}\cdot cos10-\dfrac{\sqrt{3}}{2}\cdot sin10\right)}{sin20}=\dfrac{sin\left(30-10\right)}{sin20}=1\)
10:
\(=\left(2-\sqrt{3}\right)^2+\left(2+\sqrt{3}\right)^2\)
=7-4căn 3+7+4căn 3=14
12:
\(=cos^270^0+\dfrac{1}{2}\left[cos60-cos140\right]\)
\(=cos^270^0+\dfrac{1}{2}\cdot\dfrac{1}{2}-\dfrac{1}{2}\cdot2cos^270^0+\dfrac{1}{.2}\)
=1/4+1/2=3/4

1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t

1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25


1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp

a) \(\left\{{}\begin{matrix}2x-7>0.\\5x+1>0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x>7.\\5x>-1.\end{matrix}\right.\) \(\left\{{}\begin{matrix}x>\dfrac{7}{2}.\\x>\dfrac{-1}{5}.\end{matrix}\right.\)
\(\Rightarrow x>\dfrac{7}{2}.\) \(\Rightarrow x\in\left(\dfrac{7}{2};+\infty\right).\)
Kết luận: Tập nghiệm của hệ bất phương trình trên là \(x\in\left(\dfrac{7}{2};+\infty\right).\)
b) \(\left\{{}\begin{matrix}\left(2x+3\right)\left(x-1\right)>0.\\7x-5< 0.\end{matrix}\right.\) \(\Leftrightarrow\text{}\text{}\)\(\left\{{}\begin{matrix}\left(2x+3\right)\left(x-1\right)>0.\left(1\right)\\x< \dfrac{5}{7}.\left(2\right)\end{matrix}\right.\)
Xét (1):
\(2x+3=0.\Leftrightarrow x=\dfrac{-3}{2}.\\ x-1=0.\Leftrightarrow x=1.\)
Bảng xét dấu:
\(x\) \(-\infty\) \(\dfrac{-3}{2}\) \(1\) \(+\infty\)
\(2x+3\) - \(0\) + | +
\(x-1\) - | - \(0\) +
\(\left(2x+3\right)\left(x-1\right)\) + \(0\) - \(0\) +
Vậy \(\left(2x+3\right)\left(x-1\right)>0.\Leftrightarrow\dfrac{-3}{2}< x< 1.\)
Kết hợp với (2).
\(\Rightarrow\) \(\dfrac{-3}{2}< x< \dfrac{5}{7}.\)
\(\Rightarrow x\in\left(\dfrac{-3}{2};\dfrac{5}{7}\right).\)
Kết luận: Tập nghiệm của hệ bất phương trình trên là \(x\in\left(\dfrac{-3}{2};\dfrac{5}{7}\right).\)


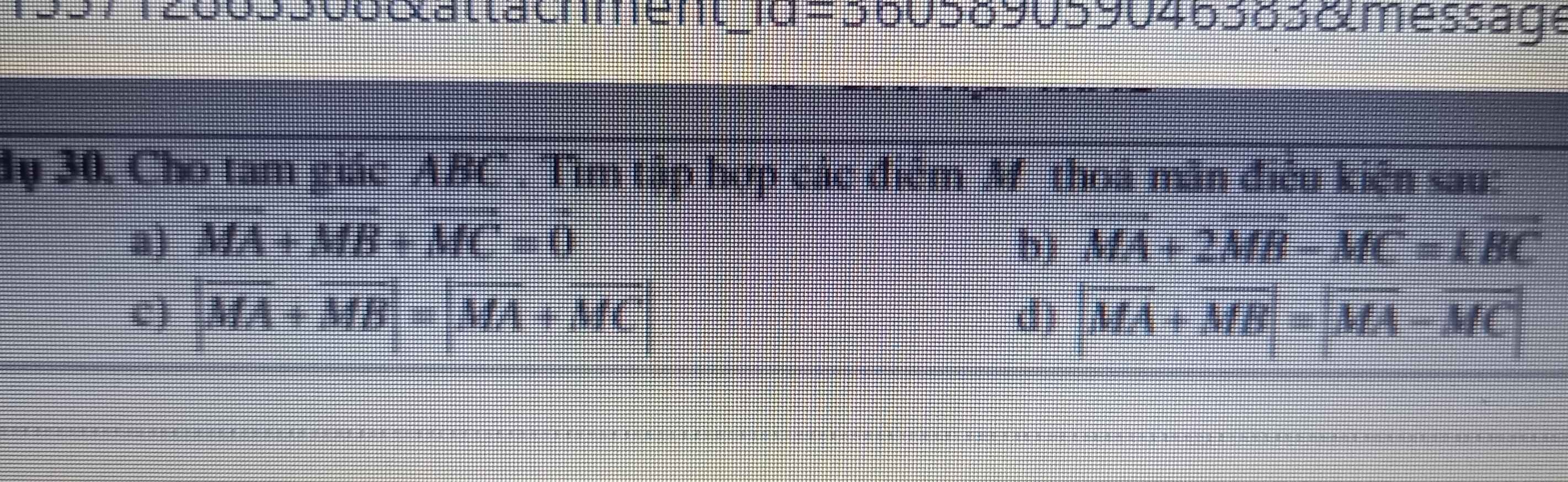



 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn


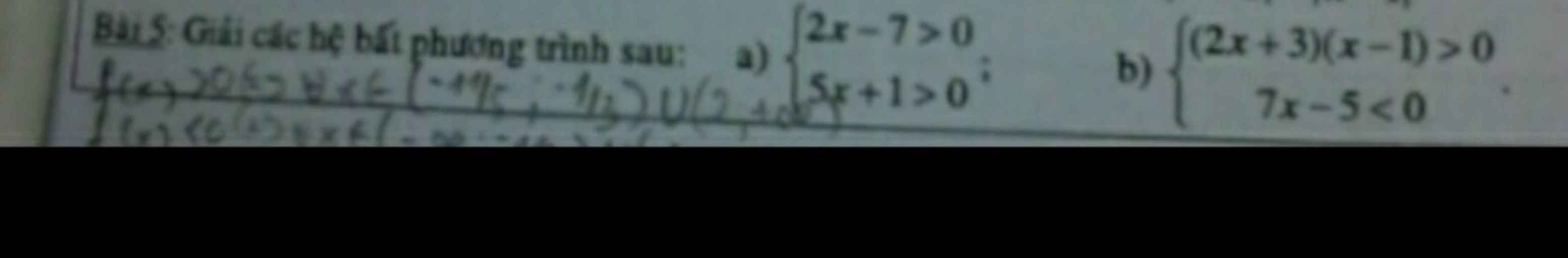

1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)