KC
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
5
TC
7 tháng 2 2020
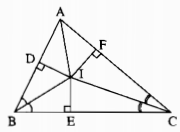
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
H
7 tháng 2 2020
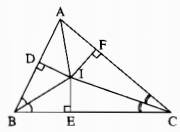
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
8 tháng 10 2021
\(\widehat{B_2}=\widehat{B_4}=60^0\left(đối.đỉnh\right)\\ \widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{B_1}=180^0-60^0=120^0\\ \Rightarrow\widehat{B_3}=\widehat{B_1}=120^0\left(đối.đỉnh\right)\)
Vì a//b nên \(\widehat{B_2}=\widehat{A_4}=60^0;\widehat{B_1}=\widehat{A_3}=120^0\left(so.le.trong\right)\)
Ta có \(\left\{{}\begin{matrix}\widehat{A_2}=\widehat{A_4}=60^0\\\widehat{A_1}=\widehat{A_3}=120^0\end{matrix}\right.\left(đối.đỉnh\right)\)
7 tháng 8 2018
khongcamxuc_123 đó nha bn bn phải giữ lời hứa đấy nha
~~~~ hok tốt ~~~~!!!!
9 tháng 11 2021
Kẻ Cp//Bm
\(\Rightarrow\widehat{BCp}=180^0-\widehat{CBm}=30^0\) (trong cùng phía)
\(\Rightarrow\widehat{DCp}=50^0-30^0=20^0\\ \Rightarrow\widehat{DCp}+\widehat{CDn}=180^0\)
Mà 2 góc này ở vị trí TCP nên Cp//Dn
Vậy Bm//Dn
9 tháng 11 2021
Kẻ Cz//Bm ta có: \(\widehat{mBC}+\widehat{BCz}=180^o\Rightarrow\widehat{BCz}=30^o\)
\(Tacó:\widehat{BCD}=\widehat{BCz}+\widehat{zCD}\Rightarrow\widehat{zCD}=20^o\)
\(\widehat{zCD}+\widehat{CDn}=20^o+160^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒Cz//Dn
Cz//Bm, Cz//Dn⇒BM//DN
