
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(2x+x^2=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
b) Ta có: \(\left(2x+1\right)^2-25=0\)
\(\Leftrightarrow\left(2x-4\right)\left(2x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

a) \(5x+10y=5\left(x+2y\right)\)
b) \(3x^2y+9xy^2z=3xy\left(x+3yz\right)\)
g) \(x^2-x-6=\left(x-3\right)\left(x+2\right)\)
h) \(x^2+9x+8=\left(x+8\right)\left(x+1\right)\)
l) \(x^2-10x+9=\left(x-1\right)\left(x-9\right)\)
k) \(x^2+x-12=\left(x+4\right)\left(x-3\right)\)
l) \(3x^2+8x+4=\left(3x+2\right)\left(x+2\right)\)

a: Ta có: \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2\)
\(=x^3-1-x^3+2\)
=1
b: ta có: \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5\)
\(=8x^3-y^3-8x^3-5\)
\(=-y^3-5\)
c: Ta có: \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2\)
\(=x^3+1-x^3+2\)
=3
d: Ta có: \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5\)
\(=8x^3+y^3-8x^3-5\)
\(=y^3-5\)
a) \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2=x^3-1-x^3+2=1\)
b) \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5=8x^3-y^3-8x^3-5=-y^3-5\)
c) \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2=x^2+1-x^3+2=3\)
d) \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5=8x^3+y^3-8x^3-5=y^3-5\)
e) \(\left(3x+2\right)\left(9x^2-6x+4\right)-27x^3-7=27x^3+8-27x^3-7=1\)
f) \(\left(3x-2\right)\left(9x^2+6x+4\right)-27x^3-7=27x^3-8-27x^3-7=-15\)



Em cần giúp câu nào hả em? Em nên chụp 1-2 ý cho 1 lần hỏi nhá, như thế mọi người sẽ dễ dàng giúp em hơn
13
a, \(3x-4=-x+8\)
\(< =>3x+x=8+4\)
\(< =>4x=12\)
\(< =>x=\frac{12}{4}=3\)
b, \(\frac{2x+1}{6}+\frac{x-7}{12}=10\)
\(< =>\frac{2\left(2x+1\right)}{12}+\frac{x-7}{12}=\frac{120}{12}\)
\(< =>4x+2+x-7=120\)
\(< =>5x=120+5=125\)
\(< =>x=\frac{125}{5}=\frac{5^3}{5}=5^2=25\)

a, Xét ΔBHA và ΔBAC có :
\(\widehat{A}=\widehat{H}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta BHA\sim\Delta BAC\left(g-g\right)\)
b, Xét ΔCHA và ΔCAB có :
\(\widehat{A}=\widehat{H}=90^0\)
\(\widehat{C}:chung\)
\(\Rightarrow\Delta CHA\sim\Delta CAB\left(g-g\right)\)
c, Xét ΔAHB và ΔCHA có :
\(\widehat{BHA}=\widehat{CHA}=90^0\)
\(\widehat{B}=\widehat{HAC}\left(phụ\cdot với\cdot\widehat{C}\right)\)
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(g-g\right)\)

\(a,=\dfrac{4xy-1-2xy+1}{5x^2y}=\dfrac{6xy}{5x^2y}=\dfrac{6}{5x}\\ b,=\dfrac{x^2+8x-2x+8}{x\left(x-4\right)\left(x+4\right)}=\dfrac{\left(x+2\right)\left(x+4\right)}{x\left(x-4\right)\left(x+4\right)}=\dfrac{x+2}{x\left(x-4\right)}\\ c,=\dfrac{x^2+3x-x+1}{x\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x+1\right)^2}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x\left(x-1\right)}\\ d,=\dfrac{x-3-x-3-2x}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{3-x}\\ e,=\dfrac{x+1-1}{x+1}=\dfrac{x}{x+1}\\ f,=\dfrac{3x+5-5+9x}{6x^2y}=\dfrac{12x}{6xy}=\dfrac{2}{y}\)
\(g,=\dfrac{x^2+6x-2x+4}{x\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x+2}{x\left(x-2\right)}\\ h,=\dfrac{3x+1-3x+1+2x-3}{\left(3x-1\right)\left(3x+1\right)}=\dfrac{2x-1}{\left(3x-1\right)\left(3x+1\right)}\\ j,=\dfrac{5x+30+x^2-30}{x\left(x+6\right)}=\dfrac{x^2+5x}{x^2+6x}\\ k,=\dfrac{\left(x-7\right)\left(x+7\right)}{2x+1}\cdot\dfrac{-3}{x-7}=\dfrac{-3\left(x+7\right)}{2x+1}\\ l,=\dfrac{x\left(3x-2\right)}{x^2-1}\cdot\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{\left(3x-2\right)^3}=\dfrac{x\left(x^2+1\right)}{\left(3x-2\right)^2}\)

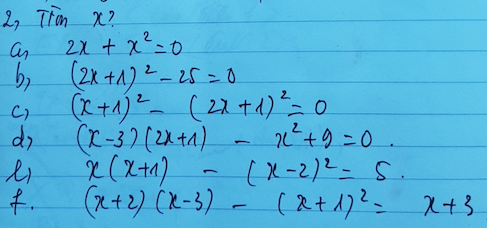
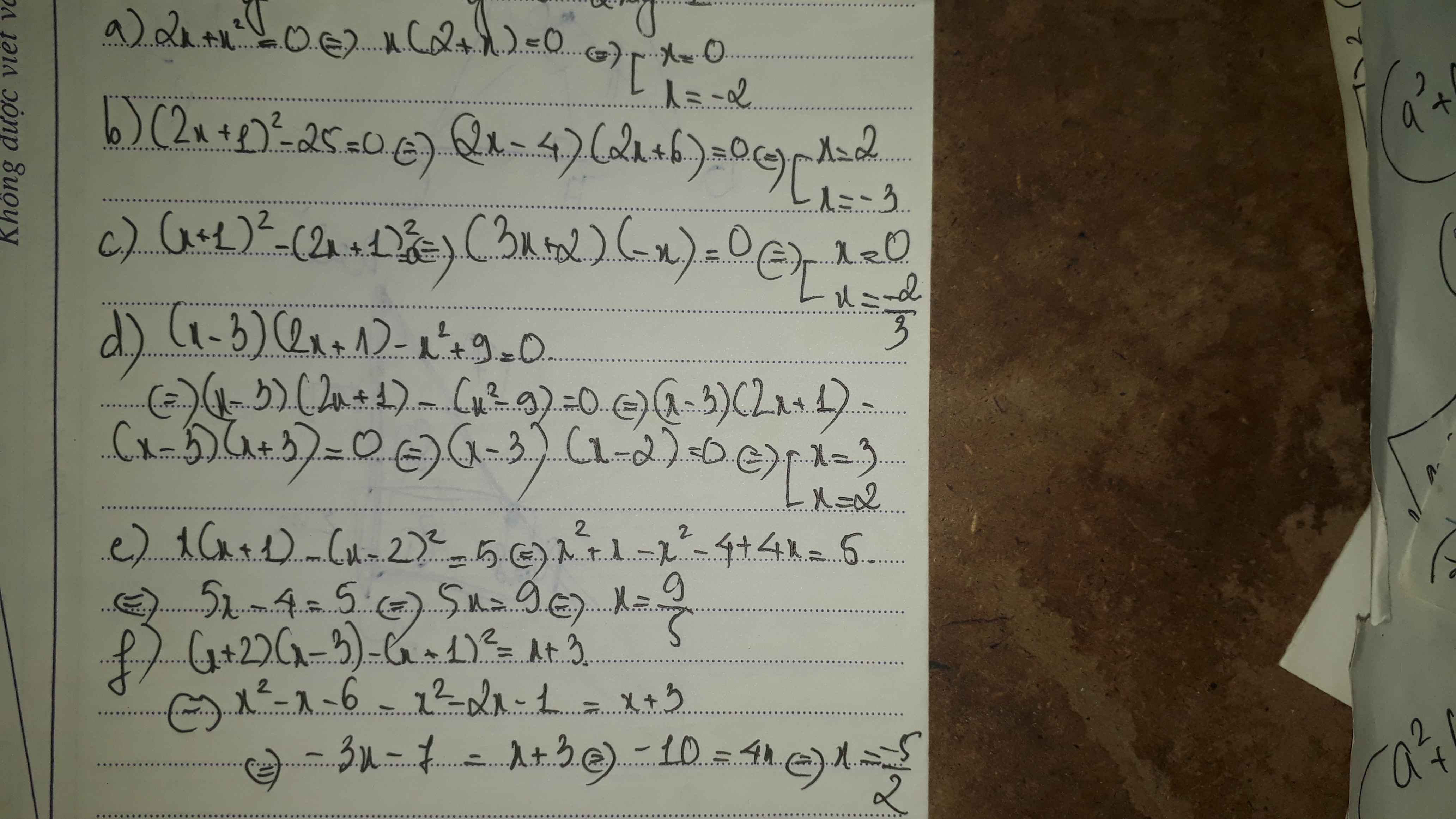
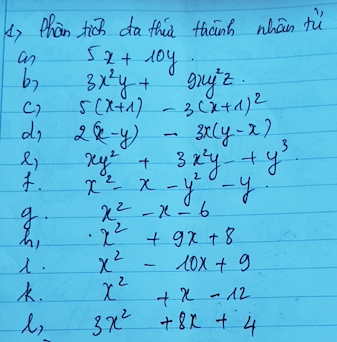


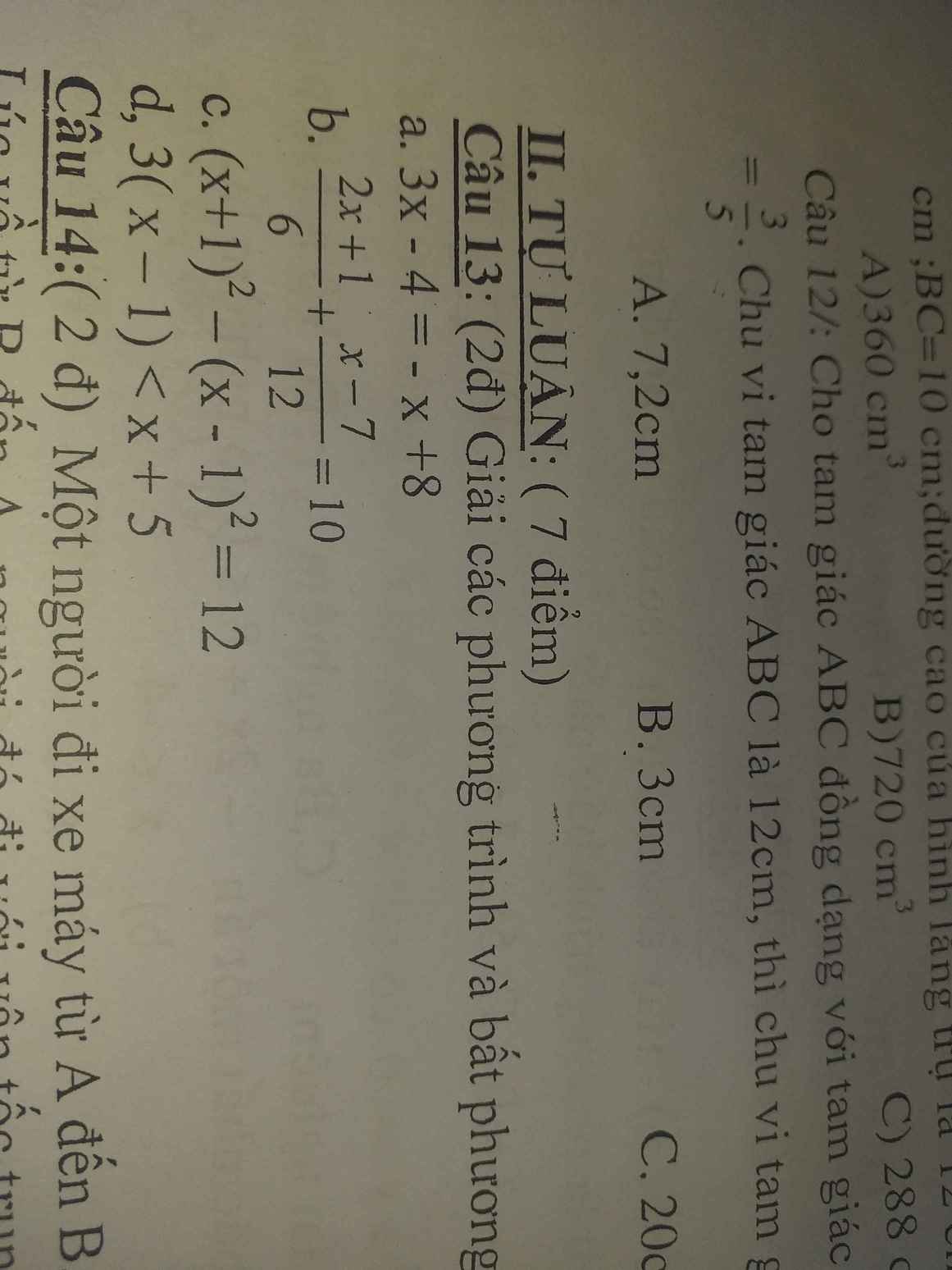

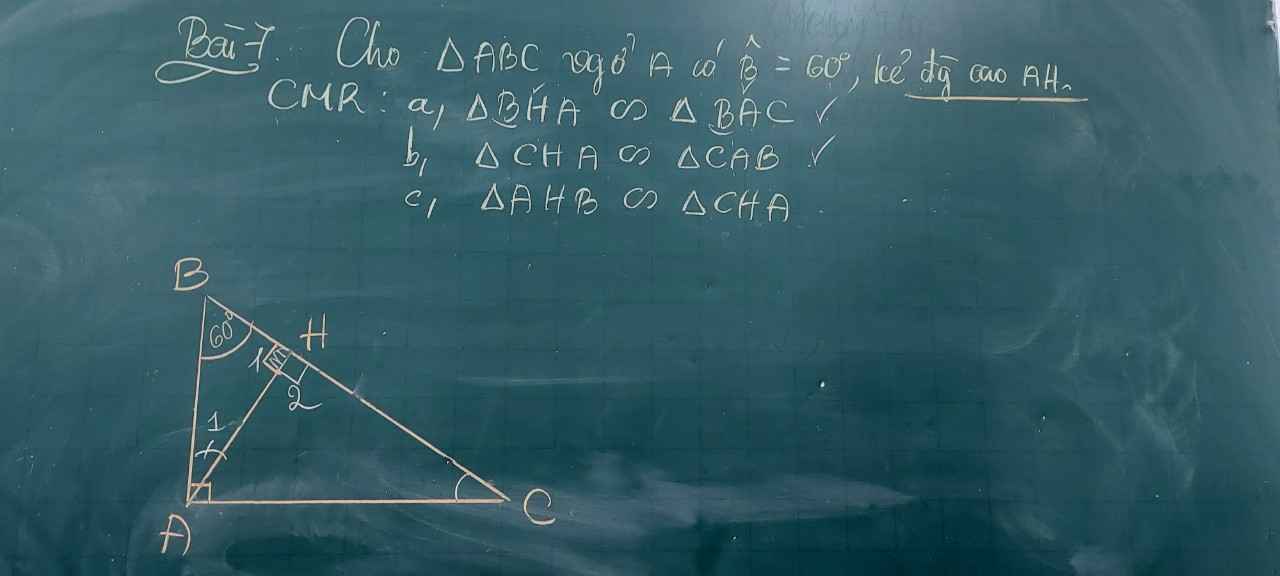
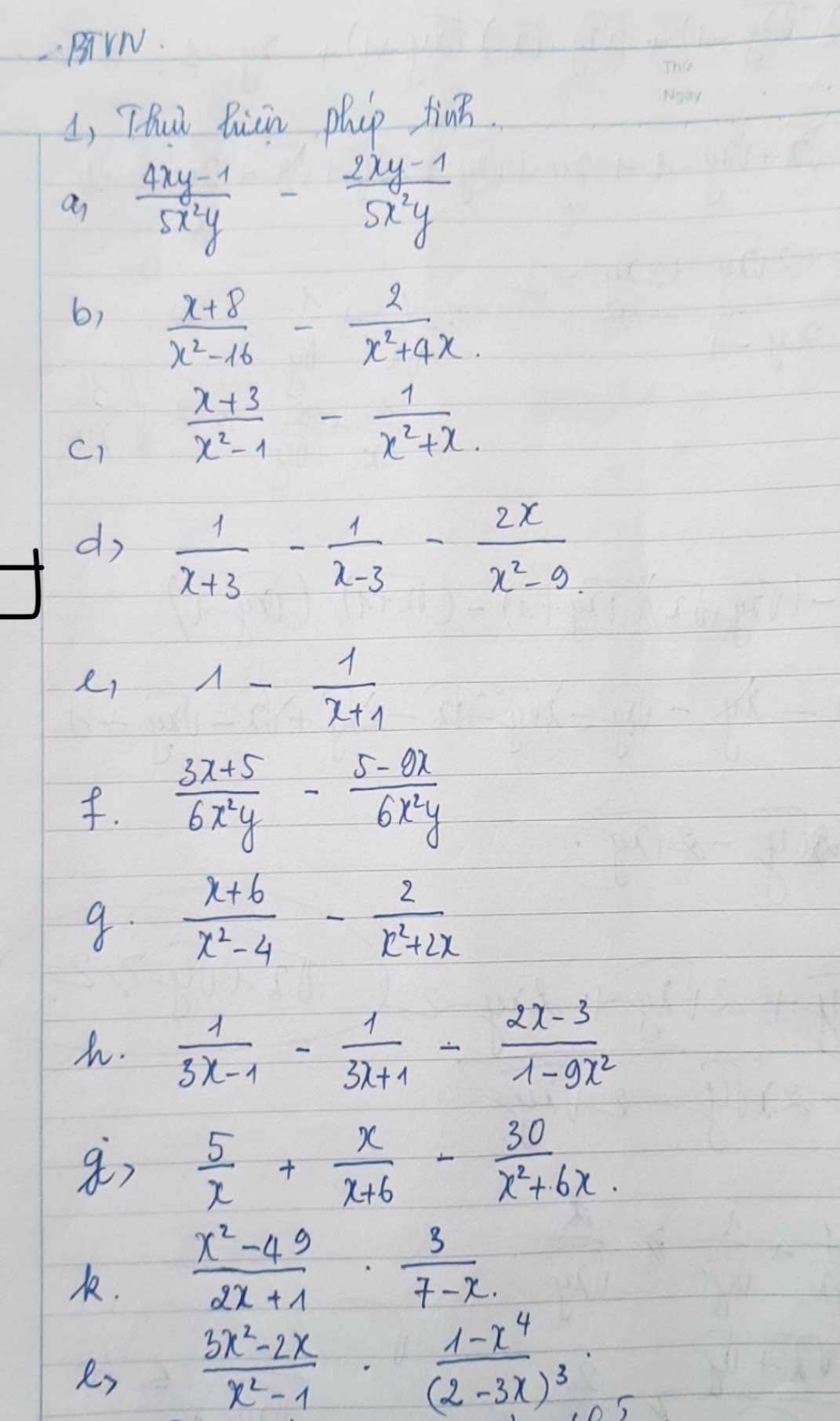
\(a,\left(2x+3\right).5x=10x^2.15x\)
\(b,1011^2-1010^2=\left(1011-1010\right)\left(1011+1010\right)=2021\)
\(c,x^2+3x=x\left(x+3\right)\)
\(c,x^2+2xy-x-2y=\left(x^2-x\right)+\left(2xy-2y\right)=x\left(x-1\right)+2y\left(x-1\right)=\left(x-1\right)\left(x+2y\right)\)
Oki thank