Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qua G kẻ đường thẳng song song AC lần lượt cắt AD, AB, BC tại E, F, N.
là giao tuyến của (GHK) và (ABCD)
Nối EH kéo dài cắt SD tại M là giao điểm SD và (NHK)
c/ Gọi P là giao điểm của FN kéo dài và CD
Ta có , mà BD qua trung điểm của AC qua trung điểm của EP là trung điểm EP
Mà MG qua trung điểm của EP MG qua trung điểm của HK hay G,M,E thẳng hàng

a: Xét ΔSAC có
H,K lần lượt là trung điểm của SA,SC
=>HK là đường trung bình
=>HK//AC
Xét (GHK) và (ABCD) có
HK//AC
\(G\in\left(GHK\right)\cap\left(ABCD\right)\)
Do đó: (GHK) giao (ABCD)=xy, xy đi qua G và xy//HK//AC
b: Chọn mp(SBD) có chứa SD
Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABC có
G là trọng tâm
BO là trung tuyến của ΔABC
Do đó: B,O,G thẳng hàng
=>G\(\in\)BD
Trong mp(SAC), gọi I là giao điểm của SO với HK
\(I\in SO\subset\left(SBD\right);I\in HK\subset\left(GHK\right)\)
=>\(I\in\left(SBD\right)\cap\left(GHK\right)\)(1)
\(G\in BD\subset\left(SBD\right);G\in\left(GHK\right)\)
=>\(G\in\left(SBD\right)\cap\left(GHK\right)\left(2\right)\)
Từ (1) và (2) suy ra \(\left(SBD\right)\cap\left(GHK\right)=GI\)
Gọi M là giao điểm của SD với GI
=>M là giao điểm của SD với (SHK)
c: Xét ΔSAC có
O,K lần lượt là trung điểm của CA,CS
=>OK là đường trung bình của ΔSAC
=>OK//SA và OK=SA/2
OK=SA/2
SH=SA/2
Do đó: OK=SH
Xét tứ giác SHOK có
SH//OK
SH=OK
Do đó: SHOK là hình bình hành
=>HK cắt SO tại trung điểm của mỗi đường
mà E là trung điểm của HK
nên Elà trung điểm của SO
=>E trùng với I
=>(SBD) giao (GHK)=GE
=>G,E,M thẳng hàng

a, đề là gì vậy bạn
b, Xét (ABCD) kẻ AI giao CD tại I
Xét (SCD); (KAG) có
K là điểm chung t1 ; I là điểm chung t2
=> KI là giao tuyến 2 mp
=> Nối IK cắt SD tại M
c, Ta có M = (SAIM) giao (GHK)
E = (HKAI) giao (GHK)
G = (HKAI) giao (SAIM)
mà ME ko song song vs MG
=> M;E;G thẳng hàng

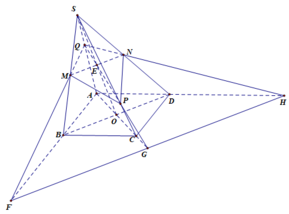
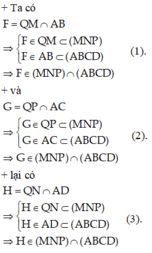
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.

a.
Do N là trọng tâm tam giác ABC \(\Rightarrow\) N là giao điểm AK và BO
Hay A,N,K,F thẳng hàng
\(\Rightarrow\left(AMN\right)\cap\left(SCD\right)=MF\)
b.
Trong mp (SCD) nối FM kéo dài cắt SD tại I
Dễ dàng nhận thấy \(SO=\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}M\in SC\in\left(SAC\right)\\M\in\left(AMN\right)\end{matrix}\right.\) \(\Rightarrow AM=\left(SAC\right)\cap\left(AMN\right)\)
\(N\in BD\in\left(SBD\right)\Rightarrow N\in\left(AMN\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}I\in SD\in\left(SBD\right)\\I\in\left(AMN\right)\end{matrix}\right.\) \(\Rightarrow IN=\left(SBD\right)\cap\left(AMN\right)\)
\(\Rightarrow\) 3 mặt phẳng (AMN), (SAC), (SBD) cắt nhau theo 3 giao tuyến phân biệt SO, AM, IN nên 3 đường thẳng này song song hoặc đồng quy
Mà SO cắt AM tại E \(\Rightarrow SO;AM;NI\) đồng quy tại E
Hay N;E;I thẳng hàng
M là trung điểm SC, O là trung điểm AC \(\Rightarrow\) E là trọng tâm tam giác SAC
\(\Rightarrow\dfrac{OE}{OS}=\dfrac{1}{3}\)
Theo giả thiết N là trọng tâm ABC \(\Rightarrow\dfrac{ON}{OB}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{OE}{OS}=\dfrac{ON}{OB}\Rightarrow EN||SB\Rightarrow NI||SB\Rightarrow NI||\left(SBC\right)\)
c.
Do \(CF||AB\), áp dụng định lý Talet:
\(\dfrac{KF}{AK}=\dfrac{KC}{KB}=1\Rightarrow KF=AK\)
Do \(AD||BK\) \(\Rightarrow\dfrac{KN}{AN}=\dfrac{BK}{AD}=\dfrac{1}{2}\Rightarrow KN=\dfrac{1}{2}AN\)
\(\Rightarrow KN=\dfrac{1}{2}\left(AK-KN\right)\Rightarrow KN=\dfrac{1}{3}AK=\dfrac{1}{3}KF\)
\(\Rightarrow KF=3KN=3\left(NF-KF\right)\)
\(\Rightarrow KF=\dfrac{3}{4}NF\)
Theo giả thiết M, K lần lượt là trung điểm SC, BC \(\Rightarrow MK\) là đường trung bình tam giác SBC
\(\Rightarrow MK||SB\Rightarrow MK||IN\) (theo c/m câu b)
Áp dụng định lý Talet:
\(\dfrac{KM}{IN}=\dfrac{KF}{NF}=\dfrac{3}{4}\Rightarrow KM=\dfrac{3}{4}IN\)
\(\Rightarrow d\left(M;AF\right)=\dfrac{3}{4}d\left(I;AF\right)\)
\(\Rightarrow\dfrac{S_{\Delta FKM}}{S_{\Delta KAI}}=\dfrac{\dfrac{1}{2}.d\left(M;KF\right).KF}{\dfrac{1}{2}d\left(I;AK\right).AK}=\dfrac{3}{4}.1=\dfrac{3}{4}\)

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



a: Chọn mp(SAB) có chứa MN
Ta có: \(AB\subset\left(SAB\right)\)
\(AB\subset\left(ABCD\right)\)
Do đó: \(\left(SAB\right)\cap\left(ABCD\right)=AB\)
Gọi P là giao điểm của MN với AB
=>P là giao điểm của MN với mp(ABCD)
b: Ta có: SN+NB=SB
=>2NB+NB=SB
=>SB=3NB
=>\(\dfrac{SN}{SB}=\dfrac{2}{3}\)
Xét ΔSBA có P,M,N thẳng hàng
nên \(\dfrac{PB}{PA}\cdot\dfrac{MA}{MS}\cdot\dfrac{NS}{NB}=1\)
=>\(\dfrac{PB}{PA}\cdot1\cdot2=1\)
=>\(\dfrac{PB}{PA}=\dfrac{1}{2}\)
=>B là trung điểm của AP
Trong mp(ABCD), gọi O là giao điểm của AC và BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAPC có
B,O lần lượt là trung điểm của AP,AC
=>BO là đường trung bình của ΔAPC
=>BO//PC
=>BD//PC
Ta có: PC//BD
BD\(\subset\)(SBD)
PC không nằm trong mp(SBD)
Do đó: PC//(SBD)

Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)
a) Để tìm giao điểm M của SD và (GHK), ta có thể sử dụng tính chất của đường thẳng và mặt phẳng. Đầu tiên, ta cần tìm phương trình đường thẳng SD và phương trình mặt phẳng GHK. Sau đó, ta giải hệ phương trình để tìm giao điểm M.
b) Để chứng minh G, E, M thẳng hàng, ta có thể sử dụng định lý về trọng tâm của tam giác và tính chất của trung điểm. Chúng ta cần chứng minh rằng G, E, M nằm trên cùng một đường thẳng.