
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé


CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)



\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3

a/ Ta có: ABCD là hình bình hành ⇒ AB // CD ⇒ \(\hat{MAO}=\hat{NCO}\); AO = OC
Xét △AMO và △CNO có:
\(\begin{matrix}\hat{MAO}=\hat{NCO}\left(slt\right)\\AO=OC\left(gt\right)\\\hat{AOM}=\hat{CON}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\begin{matrix}\Rightarrow\Delta AOM=\Delta CON\left(g.c.g\right)\\\Rightarrow OM=ON\end{matrix}\)
Vậy: M đối xứng với N qua O (đpcm).
b/ \(\begin{matrix}AO=OC\left(gt\right)\\OM=ON\left(cmt\right)\end{matrix}\). Vậy: AMCN là hình bình hành.

a: \(=\dfrac{x^2+x^2-1}{x\left(x+1\right)}:\dfrac{x^2-x^2+1}{x\left(x+1\right)}=2x^2-1\)

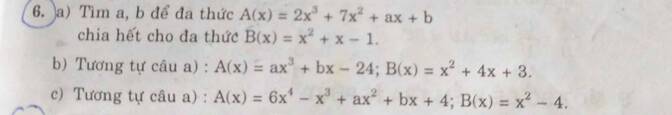



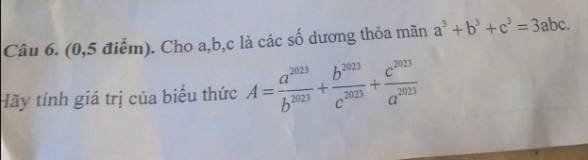

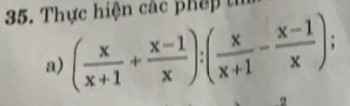
Bài 7:
a)
\(A=x\left(2x+1\right)-x^2\left(x+2\right)+x^3-x+3\\ =2x^2+x-x^3-2x^2+x^3-x+3\\ =\left(2x^2-2x^2\right)+\left(x-x\right)+\left(-x^3+x^3\right)+3\\ =3\)
Vậy ..........
b)
\(B=2x\left(x-1\right)-x\left(2x+1\right)-\left(3-3x\right)\\ =2x^2-2x-2x^2-x-3+3x\\ =\left(2x^2-2x\right)+\left(-2x-x+3x\right)-3\\ =-3\)
Vậy ...........
c)
\(C=\left(2x+11\right)\left(3x-5\right)-\left(2x+3\right)\left(3x+7\right)\\ =6x^2-10x+33x-55-\left(6x^2+14x+9x+21\right)\\ =6x^2-10x+33x-55-6x^2-14x-9x-21\\ =\left(6x^2-6x^2\right)+\left(-10x+33x-14x-9x\right)-55-21\\ =-76\)
Vậy .............
d)
\(D=x\left(2x^2-4x+8\right)+12x^2\left(\dfrac{1}{3}-\dfrac{1}{6}x\right)-8x+9\\ =2x^3-4x^2+8x+4x^2-2x^3-8x+9\\ =\left(2x^3-2x^3\right)+\left(-4x^2+4x^2\right)+\left(8x-8x\right)+9\\ =9\)
Vậy ...............
`HaNa♬D`
Bài 7.
\(a,A=x\left(2x+1\right)-x^2\left(x+2\right)+x^3-x+3\)
\(=2x^2+x-x^3-2x^2+x^3-x+3\)
\(=\left(-x^3+x^3\right)+\left(2x^2-2x^2\right)+\left(x-x\right)+3\)
\(=3\)
⇒ Giá trị của A không phụ thuộc vào giá trị của biến
\(b,B=2x\left(x-1\right)-x\left(2x+1\right)-\left(3-3x\right)\)
\(=2x^2-2x-2x^2-x-3+3x\)
\(=\left(2x^2-2x^2\right)+\left(-2x-x+3x\right)-3\)
\(=-3\)
⇒ Giá trị của B không phụ thuộc vào giá trị của biến
\(c,C=\left(2x+11\right)\left(3x-5\right)-\left(2x+3\right)\left(3x+7\right)\)
\(=6x^2-10x+33x-55-\left(6x^2+14x+9x+21\right)\)
\(=6x^2+23x-55-6x^2-23x-21\)
\(=\left(6x^2-6x^2\right)+\left(23x-23x\right)+\left(-55-21\right)\)
\(=-76\)
⇒ Giá trị của C không phụ thuộc vào giá trị của biến
\(d,D=x\left(2x^2-4x+8\right)+12x^2\left(\dfrac{1}{3}-\dfrac{1}{6}x\right)-8x+9\)
\(=2x^3-4x^2+8x+4x^2-2x^3-8x+9\)
\(=\left(2x^3-2x^3\right) +\left(-4x^2+4x^2\right)+\left(8x-8x\right)+9\)
\(=9\)
⇒ Giá trị của D không phụ thuộc vào giá trị của biến
#Urushi