K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
1
29 tháng 12 2023
\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3
NV
1
10 tháng 10 2021
\(P=\dfrac{x^3-y^3}{x^2y-xy^2}-\dfrac{x^3+y^3}{x^2y+xy^2}-\left(\dfrac{x}{y}-\dfrac{y}{x}\right)\left(\dfrac{x+y}{x-y}-\dfrac{x-y}{x+y}\right)\)
\(=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{xy\left(x-y\right)}-\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{xy\left(x+y\right)}-\dfrac{x^2-y^2}{xy}\cdot\dfrac{x^2+2xy+y^2-x^2+2xy-y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+xy+y^2-x^2+xy-y^2}{xy}-\dfrac{\left(x-y\right)\left(x+y\right)}{xy}\cdot\dfrac{4xy}{\left(x-y\right)\left(x+y\right)}\)
\(=2-4=-2\)
NV
1
22 tháng 10 2021
a: \(AO=\dfrac{1}{2}AC\)(O là trung điểm của AC)
nên AO=AD
hay ΔAOD cân tại A
NT
7
LH
27 tháng 9 2016
tình GTNN hay GTLN đều áp dụng hằng đẳng thức cơ bản và nâng cao, nếu học thoe lớp chuyên thì áp dụng cả những thứ trên trời dưới đất, trong ao ngoài hồ cũng có (vì mình học theo lớp đó) nhưng có thể phân biệt như sau
GTNN xảy ra khi có 1 số mũ chẵn + 1 số nào đó thì GTNN sẽ bằng số đó (VD tông quát là a2n+k(trong đó a có thể là 1 biểu thức, k là số bất kỳ)
GTLN xảy ra khi 1 số mũ lẻ + 1 số nào đó thì số mũ lẻ ấy phải = 0 để GTLN đạt được là cái số ko có biến đó (VD tổng quát a2n+1+k(trong đó a có thể là 1 biểu thức)
hơi khó hiểu nhỉ, ko hiểu chỗ nào cứ hỏi
6 tháng 11 2021
\(P=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{x-y}{2xy}\cdot\dfrac{y\left(x+y\right)+y\left(x-y\right)}{x\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{xy+y^2+xy-y^2}{2x^2y\left(x+y\right)}\)
\(=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{1}{x\left(x+y\right)}=\dfrac{1}{x}\)
17 tháng 10 2021
10: \(16x^2-y^2=\left(4x-y\right)\left(4x+y\right)\)
11: \(6x^2-11x+3\)
\(=6x^2-9x-2x+3\)
\(=\left(2x-3\right)\left(3x-1\right)\)
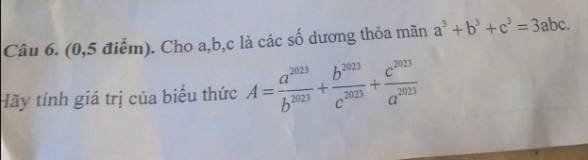
a/ Ta có: ABCD là hình bình hành ⇒ AB // CD ⇒ \(\hat{MAO}=\hat{NCO}\); AO = OC
Xét △AMO và △CNO có:
\(\begin{matrix}\hat{MAO}=\hat{NCO}\left(slt\right)\\AO=OC\left(gt\right)\\\hat{AOM}=\hat{CON}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\begin{matrix}\Rightarrow\Delta AOM=\Delta CON\left(g.c.g\right)\\\Rightarrow OM=ON\end{matrix}\)
Vậy: M đối xứng với N qua O (đpcm).
b/ \(\begin{matrix}AO=OC\left(gt\right)\\OM=ON\left(cmt\right)\end{matrix}\). Vậy: AMCN là hình bình hành.