Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Không gian mẫu là 8 3
Có hai trường hợp
+ Trường hợp 1: Bước 1 đi 4 ô góc thì bước 2 có 2 cách đi, bước 3 có 1 cách đi
+ Trường hợp 2: Bước 1 đi 4 ô còn lại thì bước 2 có 4 cách đi, bước 3 có 1 cách đi
Vậy tât cả có 4.2 + 4.4 = 24
Suy ra xác suất để sau 3 bước đi quân vua trở về ô ban đầu là: 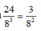

Chọn A
Ta đánh số các vị trí từ 1 đến 8.
Số phần tử không gian mẫu là ![]()
Gọi A là biến cố: “xếp được tám bạn thành hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau”.
TH1: Quân đứng vị trí 1 hoặc 8 => có 2 cách
Chọn một trong 3 bạn nam xếp vào vị trí 8 hoặc 1 còn lại => có 3 cách.
Xếp 2 bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau
=> có 6 cách
Xếp vị trí bạn Lan có 3 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: 2.3.6.3.3! = 648 cách
TH2: Chọn 2 bạn nam ( khác Quân) đứng vào 2 vị trí 1 hoặc 8 có A 3 2 cách.
Xếp Quân và bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau => có 6 cách
Xếp vị trí bạn Lan có 2 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: ![]()
![]()
Vậy xác suất của biến cố A là ![]()

Đáp án D
Phương pháp :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω |
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu » . Tính |A| .
Cách giải :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω | = 8 3 .
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu »
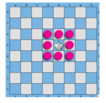
TH1: Quân vua di chuyển bước thứ nhất sang ô đen liền kề (được tô màu đỏ) có 4
cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 4 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.4 = 16 cách.
TH2: Quân vua di chuyển bước thứ nhất sang các ô trắng liền kề (được tô màu đỏ) có
4 cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 2 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.2 = 8 cách
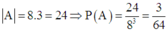

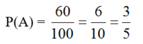
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai
+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;
⇒ n(Ω) = 10.10 = 100.
A: “ Quả cầu lấy từ hộp thứ nhất trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B
⇒ n(A) = 6.10 = 60.
B: “Quả cầu lấy từ hộp thứ hai trắng”
⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A
⇒ n(B) = 4.10 = 40.
A.B: “Cả hai quả cầu lấy ra đều trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B
⇒ n(A.B) = 6.4 = 24.
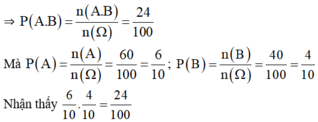
hay P(A.B) = P(A).P(B)
⇒ A và B là biến cố độc lập.
b) Gọi C: “Hai quả cầu lấy ra cùng màu”.
Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”
B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”
⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”
Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)
Và C=(A.B)∪(A−.B−)
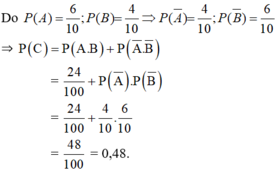
c) C− : “Hai quả cầu lấy ra khác màu”
⇒ P(C− )=1-P(C)=1-0,48=0,52