Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(\widehat{CBD}=\widehat{BDA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
Xét tứ giác ABCD có AD//BC
nên ABCD là hình thang

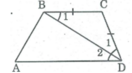
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.
⇒ ∠ B 1 = ∠ D 1 (tính chất tam giác cân)
Mà ∠ D 1 = ∠ D 2 ( Vì DB là tia phân giác của góc D)
Suy ra: ∠ B 1 = ∠ D 2
Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)
Vậy ABCD là hình thang.

ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang

Ta có hình vẽ:
Ta có: BC= CD (gt)
=> \(\Delta BCD\) cân tại C
=> góc B1 = góc D1
mà góc D1 = D2 (gt)
=> góc D2 = góc B1
mặt khác 2 góc D2 và B1 đang ở vị trí so le trong
=> AB // CD
=> tứ giác ABCD là hình thang

Vì BC=CD=>Tam giác BCD cân tại C=>\(\widehat{CBD}=\widehat{CDB}\)(1)
Vì DB là tia phân giác của góc D => \(\widehat{CDB}=\widehat{ADB}\)(2)
Từ (1) và (2) => \(\widehat{CBD}=\widehat{ADB}\),mà 2 góc ở vị trí so le trong
=> AD song song với BC.
=> ABCD là hình thang.

Bài mình làm cực chi tiết nên có một số chỗ viết tắt: gt:giả thiết, dhnb:dấu hiệu nhận biết, đ/n:định nghĩa, cmt:chứng minh trên, t/c: tính chất
3. a) Vì tam giác ABC vuông cân ở A (gt)=> góc ACB=45 độ.
tam giác ACE vuông cân ở E (gt)=> góc EAC=45 độ.
mà góc EAC và góc ACB ở vị trí so le trong.
Từ 3 điều trên=> AE//BC (dhnb) => AECB là hình thang (đ/n) mà góc AEC=90 độ (tam giác ACE vuông cân) => AECB là hình thang vuông.
b) Vì AECB là hình thàng vuông(cmt) mà góc AEC= 90 độ (tam giác ACE vuông cân). => góc ACE=90 độ.
Có: góc ABC= 45 độ (cmt).
tam giác AEC vuông cân ở E (gt)=> góc EAC=45 độ (t/c) mà góc BAC+ góc EAC= góc BAE và góc BAC= 90 độ (tam giác BAC vuông cân)=> góc BAE= 90 độ=45 độ= 135 độ.
Gọi AD là đường trung trực tam giác ABC=> AD=BD=BC=1/2BC=1/2*2=1 cm (chỗ này là tính chất tam giác vuông: trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền nhé). [đây là điều thứ nhất suy ra được]
=> AD vông góc với BC. [đây là điều thứu hai suy ra được]
Xét tam giác ADC vuông tại D (AD vuông góc BC) và tam giác AEC vuông tại E (gt) có: Cạnh huyền AC chung. Góc EAC= góc BCA (cmt) => tam giác ADC= tam giác CEA (ch-gn) => AD= EC ( 2 cạnh tương ứng) mà AD=1cm(cmt) => AE=1cm.
Xét tam giác ADB vuông (AD vuông góc BC) có: AD2+ BD2 = AB2 ( định lí Pytago)
12 + 12 =AB2 => 1+1=AB2 => Ab bằng căn bậc hai cm.
