Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vui mak, bạn dis bài mk trg khi bài mk đúng, vui quá mak
cái loại hạ đẳng thì chỉ có vậy thôi, mak thôi cx đúng súc vật đc z là hiếm lắm oy

bài 1
\(\widehat{B}=90-\widehat{C}=90-30=60\)
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{30}{sin30}=60\)
áp dụng pytago vào \(\Delta ABC\)
\(AC=\sqrt{BC^2-AB^2}\)=\(\sqrt{60^2-30^2}\)=\(30\sqrt{3}\)=51,96
bài 2
\(\widehat{B}=90-\widehat{C}=90-30=60\)
\(sinC=\dfrac{AB}{BC}\Rightarrow AB=sinC.BC=sin30.5=2,5\)
áp
áp dụng pytago vào \(\Delta ABC\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-2,5^2}\)=4,33
bài 3
\(\widehat{E}=90-\widehat{F}=90-47=43\)
\(sinF=\dfrac{ED}{EF}\Rightarrow EF=\dfrac{ED}{sinF}=\dfrac{9}{sin47}=12,31\)
áp dụng pytago vào \(\Delta DEF\)
\(DF=\sqrt{EF^2-ED^2}=\sqrt{12,31^2-9^2}\)=8,4
bài 4
áp dụng pytago vào \(\Delta ABC\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{32^2-27^2}=17,18\)
\(sinB=\dfrac{AC}{BC}=\dfrac{27}{32}\Rightarrow\widehat{B}=57\)
\(\widehat{C}=90-\widehat{B}=90-57=33\)

\(1,\\ a,=\dfrac{\left(3+2\sqrt{3}\right)\sqrt{3}}{3}+\dfrac{\left(2+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{1}\\ =\dfrac{3\sqrt{3}+6}{3}+\sqrt{2}=\sqrt{3}+1+\sqrt{2}\\ b,=\left(\dfrac{\sqrt{5}+\sqrt{2}}{3}-\dfrac{\sqrt{5}-\sqrt{2}}{3}+1\right)\cdot\dfrac{1}{\left(\sqrt{2}+1\right)^2}\\ =\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\cdot\dfrac{1}{\left(\sqrt{2}+1\right)^2}\\ =\dfrac{2\sqrt{2}+3}{3\left(3+2\sqrt{2}\right)}=\dfrac{1}{3}\)
\(2,\\ A=2x+\sqrt{\left(x-3\right)^2}=2x+\left|x-3\right|\\ =2\left(-5\right)+\left|-5-3\right|=-10+8=-2\\ B=\dfrac{\sqrt{\left(2x+1\right)^2}}{\left(x-4\right)\left(x+4\right)}\left(x-4\right)^2=\dfrac{\left|2x+1\right|\left(x-4\right)}{x+4}\\ B=\dfrac{17\cdot4}{12}=\dfrac{17}{3}\)

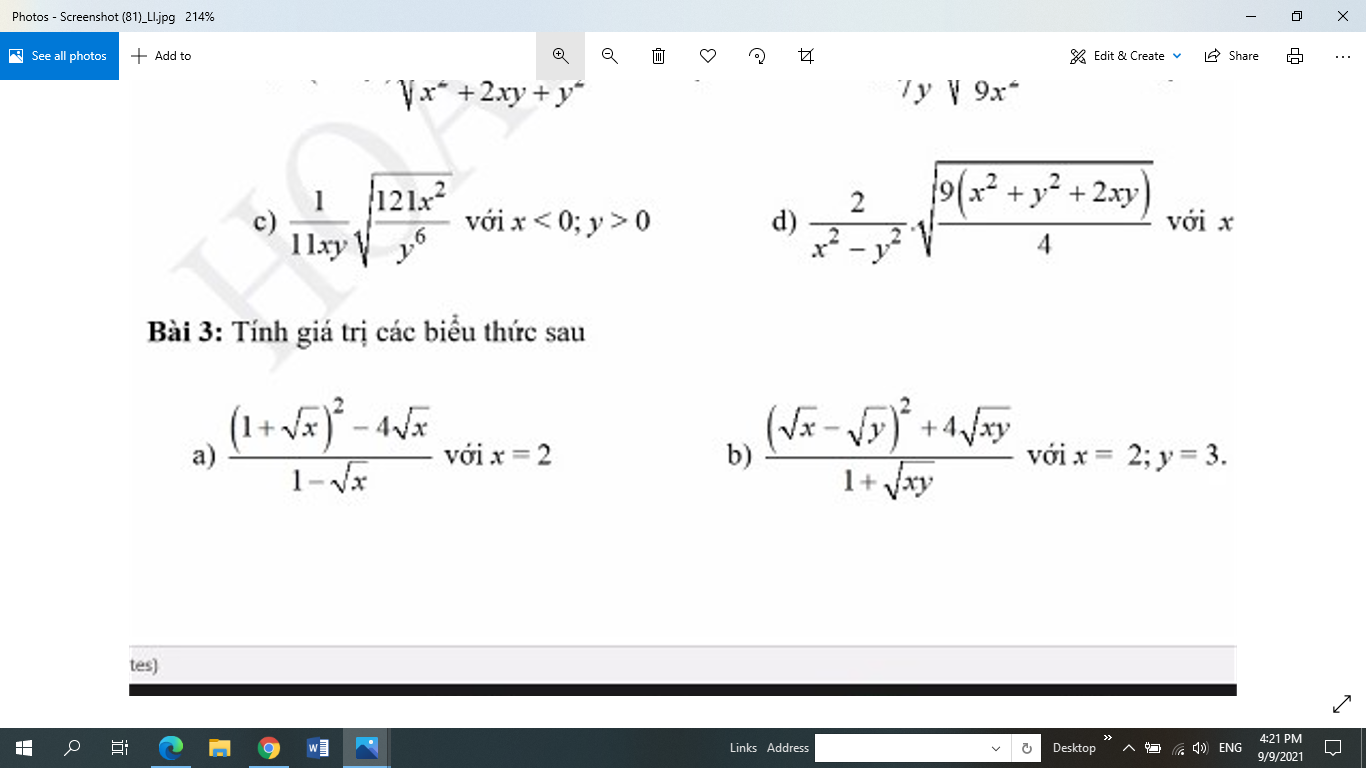
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)

sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)

a. \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{x-2\sqrt{x}}\right)\cdot\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{4}{x-4}\right)\)
<=> \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right)\cdot\dfrac{\sqrt{x}-2+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
<=> \(P=\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
<=> \(P=\dfrac{\sqrt{x}+2}{x-2\sqrt{x}}\)
b. Khi \(x=7+4\sqrt{3}=\left(2+\sqrt{3}\right)^2\) => \(\sqrt{x}=2+\sqrt{3}\)
=> \(P=\dfrac{2+\sqrt{3}+2}{7+4\sqrt{3}-2\left(2+\sqrt{3}\right)}=\dfrac{4+\sqrt{3}}{7+4\sqrt{3}-4-2\sqrt{3}}=\dfrac{4+\sqrt{3}}{3+2\sqrt{3}}=\dfrac{5\sqrt{3}-6}{3}\)
check giùm mik

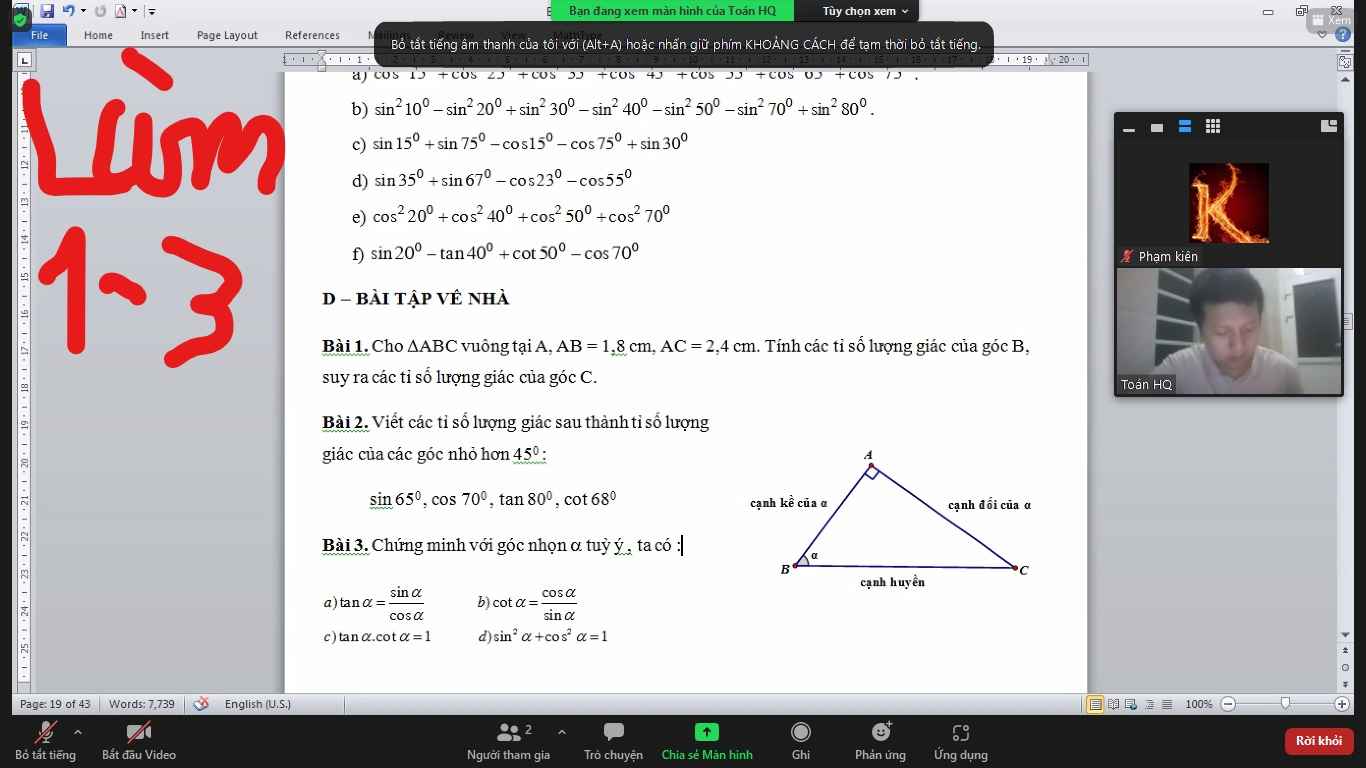
Bài 2:
\(\sin65^0=\cos25^0\)
\(\cos70^0=\sin20^0\)
\(\tan80^0=\cot10^0\)
\(\cot68^0=\tan22^0\)

Bài 1:
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=1.8^2+2.4^2=3^2\)
hay BC=3cm
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{2.4}{3}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{1.8}{3}=\dfrac{3}{5}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{2.4}{1.8}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{1.8}{2.4}=\dfrac{3}{4}\)