PT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
2 tháng 2 2016
S = 1.2 + 2.3 + 3.4 + ... + 999.1000
<=> 3S = 1.2.3 + 2.3.3 + 3.4.3 + ... + 999.1000.3
xét 3.n.(n + 1)
= 3n.(n + 1)
= n.(n + 1)(n + 2 - n + 1)
= n.(n + 1)(n + 2) - n(n - 1)(n + 1)
thay vào S được
3S = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ... + 999.1000.1001 - 998.999.1000
=> S = 999.1000.1001 ÷ 3 = 333333000
RC
20 tháng 3 2016
Ta có: \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+.....+\frac{1}{999.1000}\)
\(=\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+...+\left(\frac{1}{999}-\frac{1}{1000}\right)\)
\(=\frac{1}{1}-\frac{1}{1000}\)
\(=\frac{999}{1000}\)
20 tháng 3 2016
1/1.2+1/2.3+1/3.4+...+1/999.1000
=1/1-1/2+1/2-1/3+1/3-1/4+...+1/999-1000
=1/1-1/1000
=999/1000
HL
1
PN
0
31 tháng 1
\(A=1\cdot2+2\cdot3+...+151\cdot152\)
\(=1\left(1+1\right)+2\left(1+2\right)+...+151\left(1+151\right)\)
\(=\left(1+2+3+...+151\right)+\left(1^2+2^2+...+151^2\right)\)
\(=\dfrac{151\left(151+1\right)}{2}+\dfrac{151\left(151+1\right)\left(2\cdot151+1\right)}{6}\)
\(=151\cdot76+\dfrac{151\cdot152\cdot303}{6}\)
\(=151\cdot76+151\cdot7676=1170552\)
\(C=2\cdot4+4\cdot6+...+2024\cdot2026\)
\(=2\cdot2\left(1\cdot2+2\cdot3+...+1012\cdot1013\right)\)
\(=4\left[1\left(1+1\right)+2\left(1+2\right)+...+1012\left(1+1012\right)\right]\)
\(=4\left[\left(1+2+...+1012\right)+\left(1^2+2^2+...+1012^2\right)\right]\)
\(=4\left[1012\cdot\dfrac{1013}{2}+\dfrac{1012\left(1012+1\right)\left(2\cdot1012+1\right)}{6}\right]\)
\(=4\left[506\cdot1013+345990150\right]\)
\(=1386010912\)
\(M=1^2+2^2+...+2024^2\)
\(=\dfrac{2024\left(2024+1\right)\cdot\left(2\cdot2024+1\right)}{6}\)
\(=2024\cdot2025\cdot\dfrac{4049}{6}\)
=2765871900
\(N=1^3+2^3+...+100^3\)
\(=\left(1+2+3+...+100\right)^2\)
\(=\left[\dfrac{100\left(100+1\right)}{2}\right]^2\)
\(=\left[50\cdot101\right]^2=5050^2\)
\(Q=1^3+2^3+...+2024^3\)
\(=\left(1+2+3+...+2024\right)^2\)
\(=\left[\dfrac{2024\left(2024+1\right)}{2}\right]^2\)
\(=\left[1012\left(2024+1\right)\right]^2\)
\(=2049300^2\)
RR
3
7 tháng 6 2018
\(\frac{\left(1.2\right)^2}{\left(2.3\right)^2}.\frac{\left(3.4\right)^2}{\left(4.5\right)^2}...\frac{\left(999.1000\right)^2}{\left(1000.1001\right)^2}\)
\(=\frac{1^2.2^2}{2^2.3^2}.\frac{3^2.4^2}{4^2.5^2}...\frac{999^2.1000^2}{1000^2.1001^2}\)
\(=\frac{1^2.2^2.3^2.4^2...999^2.1000^2}{2^2.3^2.4^2.5^2...1000^2.1001^2}\)
\(=\frac{1^2}{1001^2}\)
\(=\frac{1}{1001^2}\)
7 tháng 6 2018
\(\frac{\left(1.2\right)^2}{\left(2.3\right)^2}.....\frac{\left(999.1000\right)^2}{\left(1000.1001\right)^2}\)
\(=\frac{1^2.2^2}{2^2.3^2}.....\frac{999^2.1000^2}{1000^2.1001^2}\)
\(=\frac{1^2}{3^2}.\frac{3^2}{5^2}.....\frac{999^2}{1001^2}\)
\(=\frac{1^2}{1001^2}=\frac{1}{1002001}\)
T
1
IS
24 tháng 3 2017
a, 1/1.2+1/2.3+1/3.4+...+1/999.1000
= 1/1-1/2+1/2-1/3+1/3-1/4+....+1/999-1/1000
= 1/1-1/1000
= 999/1000
b, 1/2.4+1/4.6+1/6.8+1/8.10
= 1/2-1/4+1/4-1/6+1/6-1/8+1/8-1/10
= 1/2-1/10
= 4/10 =2/5
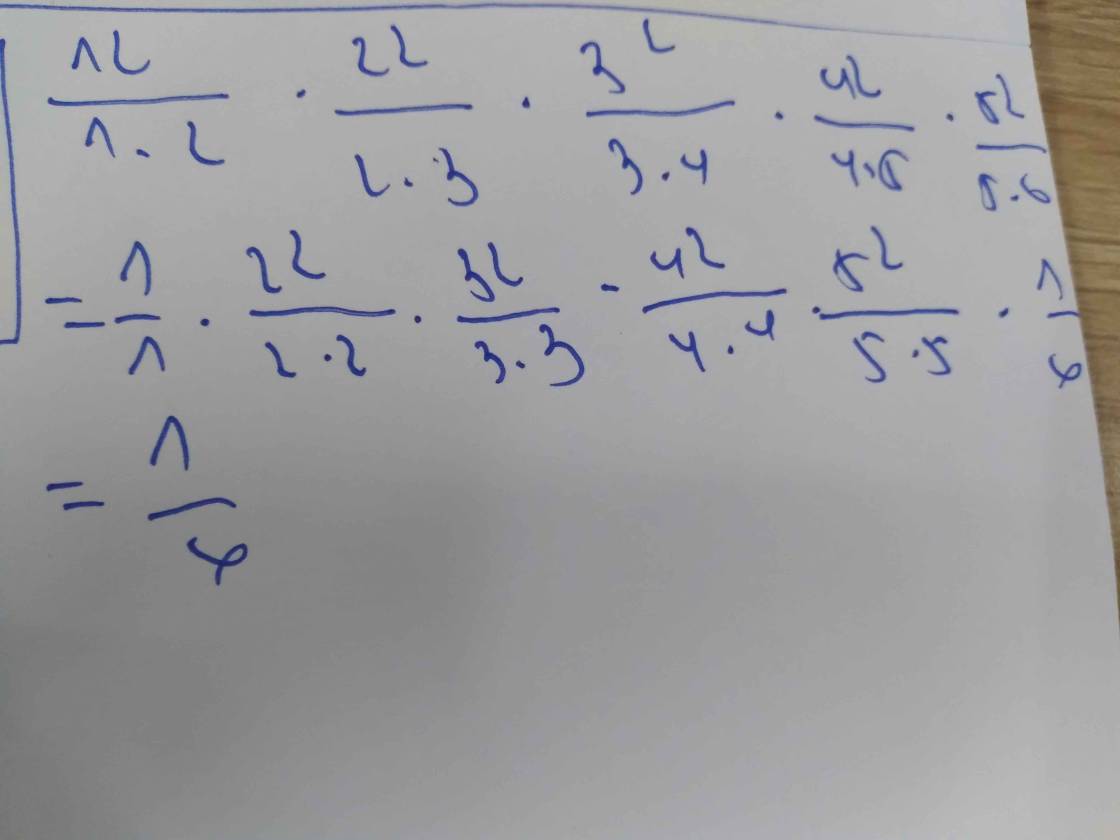
12 /1.2 . 22/2.3 . 32/3.4 ... 9992/999.1000
= 1.1/1.2 . 2.2/2.3 . 3.3/3.4........... 999.999/999.1000
= 1/2. 2/3 . 3.4.....999/1000
= 1/1000
thanks