Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phép vị tự tâm I (1; 4) tỉ số k = -2, biến M(x; y) thuộc d thành M’(x’;y’) thuộc d;
⇒ I M ' → = - 2 I M →
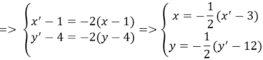
Thay vào phương trình d ta được
7. − 1 2 ( x ' − 3 ) + 3. − 1 2 ( y ' − 12 ) − 4 = 0 ⇔ 7 ( x ' − 3 ) + 3 ( y ' − 12 ) + 8 = 0 ⇔ 7 x ' + 3 y ' − 49 = 0
⇒ d' có phương trình là: 7x + 3y - 49 = 0.
Đáp án A

Dễ thấy d // d’, ta có d ∩ Oy = A(0; 1); d’ ∩ Oy = A’(0; -4). Phép đối xứng tâm I biến Oy thành Oy thì I thuộc trục Oy; biến d thành d’ thì I là trung điểm của AA’ ⇒ I(0; -3/2).
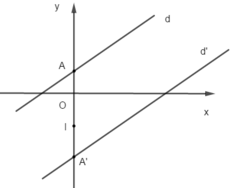
Đáp án D

Bài 1:
\(AB=\sqrt{\left(4+2\right)^2+\left(1+3\right)^2}=\sqrt{6^2+4^2}=2\sqrt{13}\)
\(A'B'=\dfrac{1}{2}\cdot AB=\dfrac{1}{2}\cdot2\sqrt{13}=\sqrt{13}\)

I M ' → = − 1 2 I M → ⇔ x − 0 = − 1 2 . ( 12 − 0 ) = − 6 y − 2 = − 1 2 ( − 3 − 2 ) = 5 2 ⇒ x = − 6 y = 9 2
Đáp án B

Phương trình đường thẳng d: x - y - 1= 0
Lấy M(x; y) thuộc d
Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì O M ' → = 3 O M → ⇔ x ' = 3 x y ' = 3 y ⇔ x = 1 3 x ' y = 1 3 y '
Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)
Thay vào phương trình d ta được: ⇔ x ' ' = x ' y ' ' = − y ' ⇔ x = 1 3 x ' ' y = − 1 3 y ' '
Hay x’’ + y’’ - 3 = 0
Vậy phương trình đường thẳng d’: x + y - 3 = 0.
Đáp án B
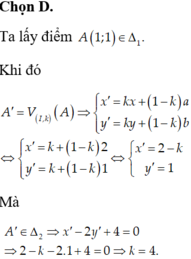

Câu 1:
Gọi M(1;0) thuộc (d)
Theo đề, ta có: \(\overrightarrow{IM'}=k\cdot\overrightarrow{IM}\)
=>\(\left\{{}\begin{matrix}x_{M'}-1=k\cdot\left(1-1\right)=0\\y_{M'}=k\cdot\left(0-0\right)=0\end{matrix}\right.\)
=>M'(1;0)
Thay M' vào x+2y+c=0, ta được:
1+c=0
=>c=-1