Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng BC vuông góc AH nên nhận (1;-3) là 1 vtpt
Phương trình BC: \(1\left(x-2\right)-3\left(y+7\right)=0\Leftrightarrow x-3y-23=0\)
Do M thuộc CM nên tọa độ có dạng \(M\left(-2m-7;m\right)\)
M là trung điểm AB \(\Rightarrow A\left(-4m-16;2m+7\right)\)
Mà A thuộc AH nên:
\(3\left(-4m-16\right)+\left(2m+7\right)+11=0\Rightarrow m=-3\Rightarrow A\left(-4;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(6;-8\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt \(\Rightarrow\) pt AB là...
C là giao điểm BC và CM nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+2y+7=0\\x-3y-23=0\end{matrix}\right.\) \(\Rightarrow C\left(5;-6\right)\Rightarrow\overrightarrow{BC}=...\Rightarrow\) phương trình BC

Ta có: 2 x + 1 > 3 x - 2 - x - 3 < 0 ⇔ - x > - 3 - x < 3 ⇔ x < 3 x > - 3 ⇔ - 3 < x < 3

a: vẽ vecto CN=vecto AB
(vecto AB;vecto CA)=(vecto CN;vecto CA)=góc ACN=120 độ
b: (vecto AB;vecto MC)
=(vecto CN;vecto CH)
=góc NCH
=120 độ

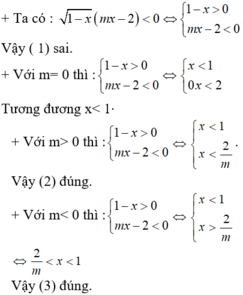

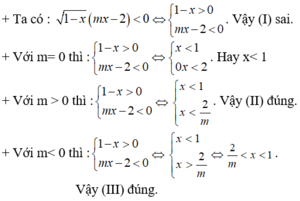
Câu 1: Số nghiệm là 1 nghiệm
Câu 4: B
Ghi cách làm dùm mình với á.😥